Room gain is not a term used in acoustics textbooks as such,it lives in the world of hi-fi without a clear definition. Sometimes it describes how the sound field from a loudspeaker is generally affected by the room, but it is seemingly often associated specifically with the sound pressure in a room around and below the first mode of the room, and that is the definition we will explore here.
What is observed in some measurements is an in-room sound pressure that is not easily explained by the anechoic response, as in the room the level extends to much lower frequencies than the characteristic frequency of the loudspeaker. This effect is a surprise to many people, and since it is not much explored in the literature, it will be approached here in steps.
Boundary Gain
Let us first build some intuition about different aspects related to sound sources in constrained spaces. Imagine first a monopole sound source S radiating into free space. For a given volume velocity the resulting sound pressure can be calculated or measured, and a certain sound power is radiated from the source.
Next, imagine the source placed up against it in an infinitely large hard boundary, where hard means that it is not moving and perfectly reflects all sound. An equivalent situation can be represented by removing the wall and adding a mirror source on top of the original source with the same source strength, and so the sound pressure is effectively doubled as the two sources are correlated. Boundary gain thus describes how restricting the solid angle that a sound source radiates into will increase the acoustic output.
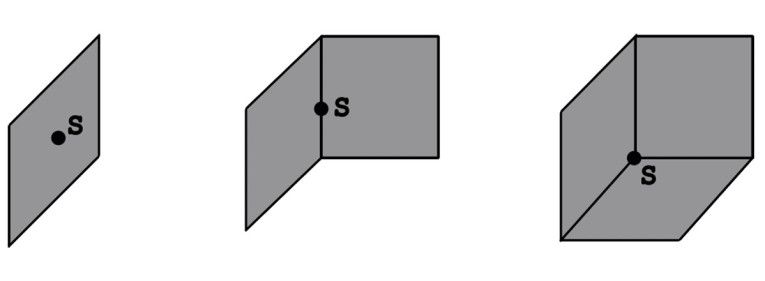
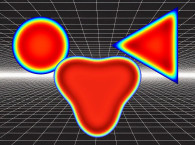
In Figure 1, three typical boundary gain situations are depicted. There is an underlying assumption that the source is omni-directional, so above a certain frequency where the source becomes more directional, the effect will be less relevant. You will sometimes see a switch on the back of some equipment where you can toggle between situations regarding the placement near a wall, and it will apply appropriate filters to lower the gain at lower frequencies because of this boundary gain. In some instances, the filters may even compensate somewhat for the speaker-boundary interferences response, which is our next topic.
Speaker-Boundary Interference Response
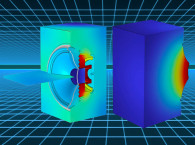
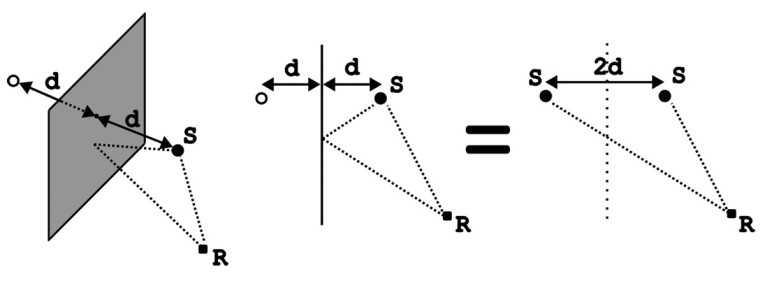
When the source is not placed directly at the infinite boundary but instead at a distance from the boundary, there are also reflections to consider, oftentimes categorized as speaker-boundary interference response (SBIR) effects in the hi-fi community. The distance from the source to the boundary as well as the frequency will affect the sound pressure in any point. The mirror source analogy can be used again to view the reflection as an added source as shown in Figure 2, and so for all frequencies one must sum over the two sources causing constructive and destructive interference.
For example, for a frequency with a wavelength of a quarter of the distance d from the source to the wall, there will be half a wavelength extra distance from the mirror source to a listening position on-axis, and so there will be a complete cancellation for the listener at this frequency, assuming hard walls.
If there are several boundaries present, there are several first reflections, and if more than first reflections are to be considered then mirror sources of mirror sources must be included. Again, the directivity of the source is important, and this directivity will depend on the frequency.
Modal Behavior
When there are enough boundaries to form a closed room, modal aspects must be considered. While the mirror analogy still holds, it becomes inconvenient to work with in practice. Instead, a modal approach is utilized. A mode, or “eigenmode,” consists of two characteristics: An eigenfrequency and an eigenfunction.
The eigenfrequency is the (angular) frequency associated with the mode, and the eigenfunction expresses the shape of the sound field associated with the mode. For a cuboid shaped room with
hard walls the eigenfrequencies can be calculated [1]:
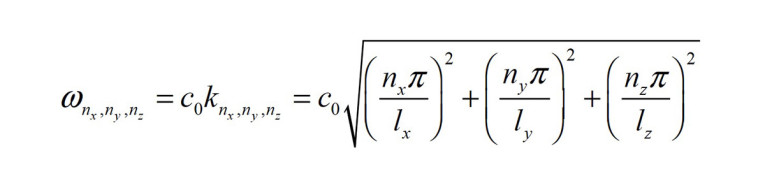
where lx, ly, and lz are the dimensions of the room in question, with sound speed c0 and indices nx, nx, and nx each from zero to
infinity. Each eigenfunction is found via:
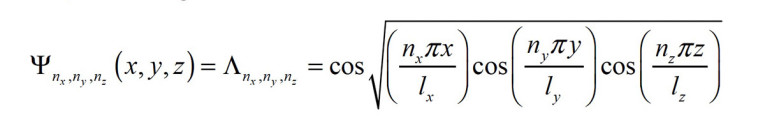
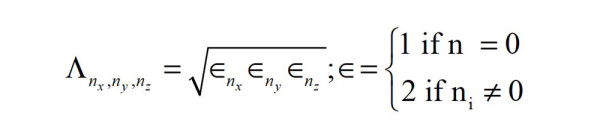
What is most important to understand when it comes to modal behavior is that modes exist independent of any source. That is how they are calculated, both analytically and numerically using Finite Element Analysis (FEA) as there is no source entered anywhere in the eigenmode setup. When sources are present in a room, all the modes have the potential to be excited, each to some degree, and so the total sound field will depend on the source type, source placement, and listener/receiver placement.
In general, the sound field in a room can be described via the pressure phasor, but it is not trivial to establish the complex coefficient A for a given situation:
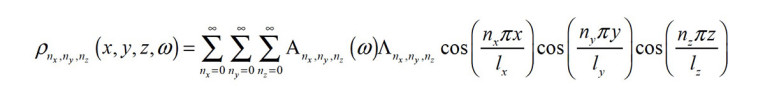
In-Room Frequency response
For a sound source (S) placed in the room and a receiver (R) placed in the listening position, the resulting complex sound pressure can be calculated either via numerical methods or via
the analytical expression:
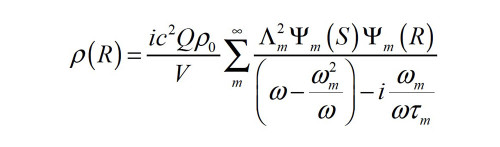
With m being a general index over all modes, and τm being a time constant to include a (small) amount of damping for each mode. As superposition holds, one can calculate the sound field from multiple subwoofers with each of their characteristics (gain, phase, characteristic frequency, quality factor Q, sealed, or ported) placed at different locations in the room by summing across several instances of the equation for a fixed listening position.
This way one can also calculate dipole and quadrupole responses by combining monopoles with certain distances and phases. Note that while the frequency response is calculated using the room modes, it is not in general possible to extract all modes from looking at a single frequency response.
Certain modes may not be significantly excited due to the placement of the source(s) and/or the receiver could be placed so that the effects of certain modes are not seen. Also note that any applicable boundary gain and SBIR effects are included in the modal calculations.
The Zeroth Mode
As we are mainly interested in understanding why there is a gain at very low frequencies, we first realize that there is a “zeroth mode” at 0Hz falling out of the above analysis. We can calculate the sound field resulting from a monopole source with volume velocity Q at very low frequencies by truncating the previous equation to index zero only:
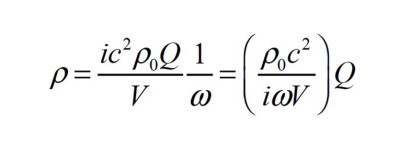
Loudspeaker Types
The final piece of the puzzle is to look at the displacement behavior of the low-frequency driver(s) in the loudspeaker for different loudspeakers; primarily the sealed enclosure and the vented enclosure with one or more ports. In general, a loudspeaker will be designed to output a constant acceleration as a function of frequency, as this will result in a constant sound pressure level (SPL) as a function of frequency. But this is in its normal operating frequency range above its resonance frequency.
For a standard electrodynamic driver in an enclosure, there will be a constant cone acceleration above the characteristic frequency of the loudspeaker, but below it will tend toward a different characteristic, depending on the enclosure type. For a sealed enclosure this will be a constant displacement at low frequencies, which is proportional to a velocity that decreases with frequency. For a vented loudspeaker, however, the displacement is not constant at low frequencies, but instead has a second-order slope corresponding to the fourth-order roll-off in its anechoic pressure.
Room Gain
We can now see where the observed room gain originates. For a sealed subwoofer, the displacement is constant as a function of frequency below the subwoofer’s characteristic frequency. So the downward slope of the acoustic impedance of the room will be countered by the velocity sloping upward with first order, resulting in a flat sound pressure response from the subwoofer below its characteristic frequency.
This is what has been discussed on many hi-fi forums, namely that the room helps retain a constant sound pressure level below the subwoofer’s own roll-off. The reason is simply that there is a zeroth mode at 0Hz, and although sound is associated with oscillation, there still is the same resonance phenomenon toward low frequencies as there is near any other excited modes.
Think of a syringe blocked on one end with a plunger in the other end. The static pressure change will be proportional to the displacement of the plunger, and this will hold dynamically also for an oscillatory displacement below the first axial eigenmode in the syringe. For a vented subwoofer the output from the rear of the driver(s) will short-circuit the front output, and so less and less pressure can be built toward 0Hz.
The roll-off for the vented subwoofer will not be the fourth order as observed under anechoic conditions, but instead second order in-room. The syringe analogy can be used again, only now there is a small hole in the barrel, preventing quasi-static pressure. The room is assumed airtight, which is not generally the case, and so the measured results will of course vary from the above ideal case. The calculated results will now be compared to measurements.


Measurements vs. Simulations
Erik Wiederholtz provided several measurements for his room, but in this article we will limit ourselves to a sealed and a vented subwoofer, respectively, placed in the front lower left corner, for a 5.7m × 4.62m × 2.67m room as shown in Photo 1, with the microphone placed in the opposite rear upper right corner as shown in Photo 2.
The simulation software COMSOL Multiphysics was used for calculating SPLs, but only because we have also been exploring the effect of adjacent rooms and leakages. The analytical expression given earlier will fully suffice in recreating the responses shown here.
The sealed subwoofer was simulated via its anechoic transfer function with a Q of 0.71 and a characteristic frequency of 33Hz. In Figure 3 the analytical results show the constant pressure at frequencies below the subwoofer’s natural roll off, and the measurements follow the same trend at low frequencies. There are no losses in the simulation, and so the resonances are very pronounced, whereas the measured results are for a room with furniture in it, and it also has a large opening into an adjacent room, and so the two responses are naturally different.
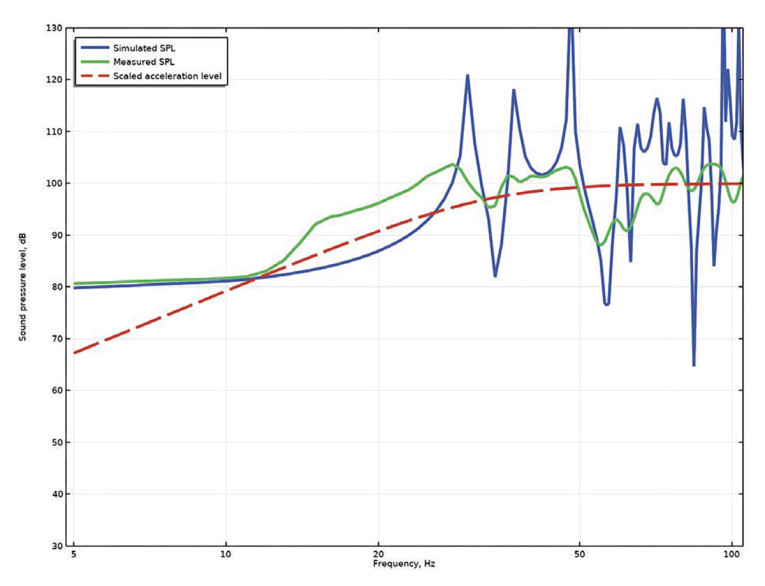
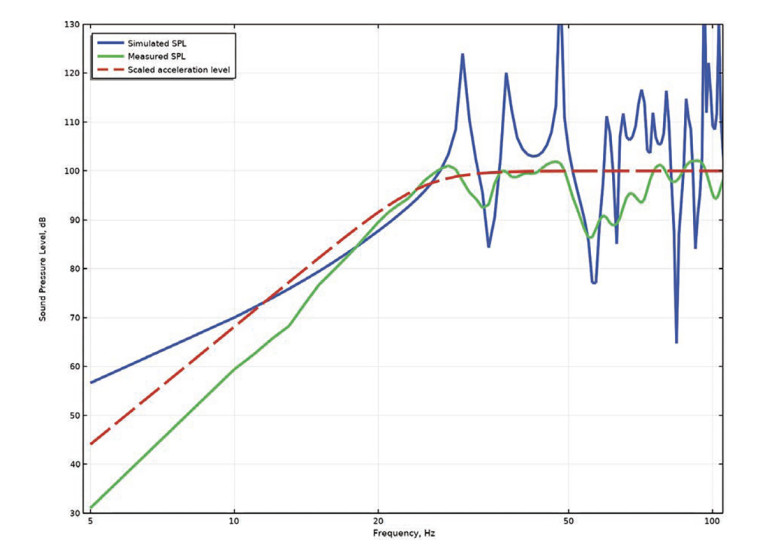
Conclusion
The elusive term “room gain” has been described via a modal approach recognizing that for an airtight room there is a “zeroth mode” that affects the very low frequency response of a loudspeaker, so that its in-room response will not match its anechoic response.
The traditional modal aspects from room acoustics do indeed capture the room gain effect, and it will show up both using the standard room acoustic equations and in numerical calculations. The room acts as an acoustic compliance, so a lumped analogy can be used for arriving at the same conclusion of the pressure being constant for a constant displacement from a sealed subwoofer at low frequencies. As rooms are not in general airtight, the effect will be seen to various degrees, but it has at least been explained now how it relates to the traditional room acoustics nomenclature. aX
Author Acknowledgements: Thanks to Erik Wiederholtz (CTO of Perlisten Audio) for some fruitful discussions and for delivering in-room measurements and photos of the room.
References
[1] F. Jacobsen, The Sound Field in a Reverberation Room, Lyngby, Denmark: Ørsted DTU, Acoustic Technology, Technical University of Denmark, 2022.
This article was originally published in audioXpress, July 2023