When looking at a frequency response from a loudspeaker driver (magnitude and phase of the pressure in a microphone point), a lot of information can be extracted regarding its behavior. The magnitude response is typically the primary focus, and a flat response here is the desired outcome, whereas the (oftentimes ignored) phase response holds information about the temporal aspects of the loudspeaker and generally of the setup regarding number of drivers and how they combine to the full response.
However, the sound pressure is simply a zero-dimensional signal, which does not necessarily tell us the whole story about the three-dimensional aspects of the surface vibration and how it generates the sound. To really dissect where, for example, dips and peaks in the pressure response come from some other tools can help, and two such tools are the Phase Decomposition and the Axial-Symmetrical Decomposition techniques, respectively.
The Phase Decomposition technique [1] as well as the Axial Symmetrical Decomposition [2] have been promoted by Klippel, where they are built into measurement systems and so can be applied to measurements only. I was involved in the development of an add-on package that could take in simulated surface (cone, dust cap, surround) displacement data, and analyze it as it had been measured. But shortly thereafter I developed a simulation setup in COMSOL Multiphysics where the phase decomposition could be carried out directly based on simulation data, and this approach has been used in the analysis and synthesis work for several clients since then.
Phase Decomposition
The first technique relies on knowing the complex pressure in a microphone point and relating the complex displacement across the loudspeaker surface to the pressure, or more specifically to the phase of said pressure. Knowing these quantities, the following displacement components can be established:
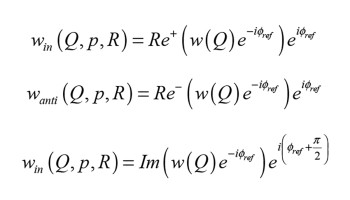
with a reference phase of:
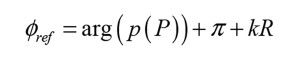
I outlined the details in two separate articles that I wrote on the subject [3] and [4], so let’s dive into these equations, starting with the last one first. Looking at the reference phase, the first part is simply the phase of the pressure in the microphone point. This is important, as this is basically the phase that we want to compare with the displacement phase. The middle part indicates a sign shift; this relates to the fact that the pressure in general correlates with the acceleration of the cone and the displacement is proportional to the negative acceleration.
The final part is basically a subtraction of the phase related to the path from the integration point Q to the microphone point P; a subtraction of the irrelevant phase coming from the time delay/transport delay. The total displacement in a point Q on the surface is denoted by w(Q), the respective in-phase, anti-phase, and quadrature components as previously listed. The in-phase displacement is the displacement that is in-phase with the reference phase, which I already explained is the pressure phase taking into account the sign and the distance aspects.
This part of the displacement adds to the total pressure. The operator Re+ returns the positive part of the real part. Basically, the equations indicate rotations, projections, and back-rotations according to Figure 1, which shows the complex displacement phasor w(Q) and the complex pressure phasor p(Q) along with the component axes.
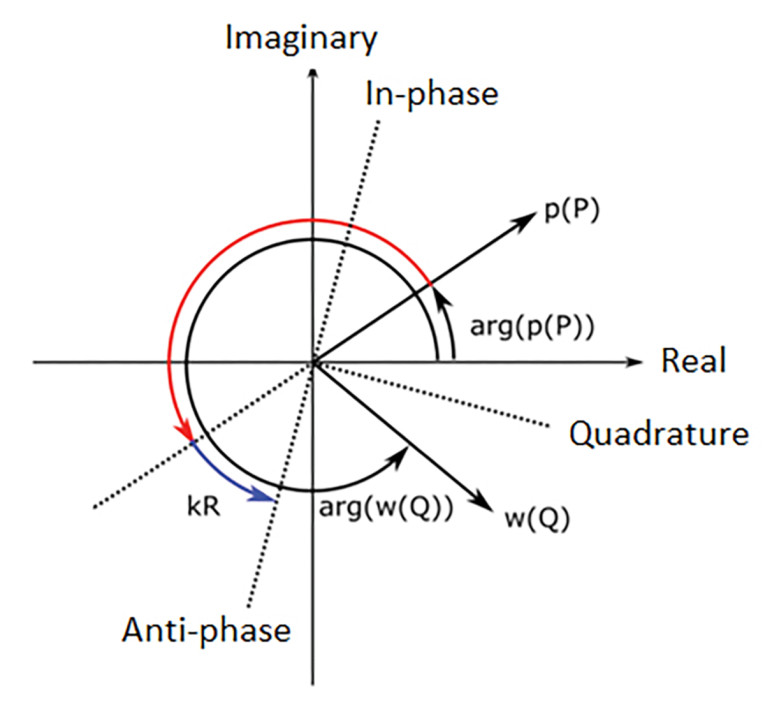
Similarly, the anti-phase displacement components subtract from the total displacement. And finally, the quadrature displacement component neither adds to nor subtracts from the total displacement, with Im being the imaginary part operator. Both the in-phase displacement and the anti-phase ditto have associated in-phase and anti-phase pressures, respectively, whereas the quadrature displacement does not affect the pressure and so has zero associated pressure.
For the Klippel implementation, the pressure is not measured, but instead calculated via the so-called Rayleigh integral:
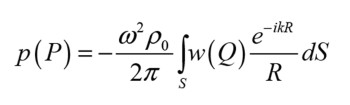
with the angular frequency ω, the density of the medium ρ0, the distance from the microphone point to the points Q on the surface under integration, and S being the entire surface to be integrated. Using the Rayleigh integral, there is an assumption that the surface is flat and placed in an infinite baffle (Figure 2).
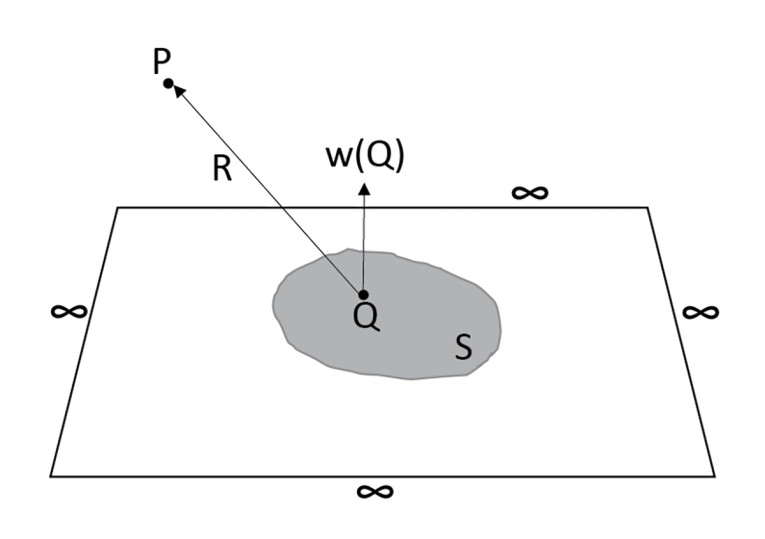
The latter requirement fits well with how the typical simulation setup is anyway, but the former is an issue, since most drivers are not flat. Still, the overall analysis and conclusion are typically of value, and a correction can be established before running the actual phase decomposition. These issues were explored in an Audio Engineering Society paper that I co-wrote with Urik Skov [5], but for each case one must evaluate the effect of not fulfilling the “flat” requirement. (One thing to note is that while the varying distance coming from varying depth on the cone is in fact included in the calculations, the dipole aspect of the full Kirchhoff-Helmholtz equation that the Rayleigh integral can be derived from, is not included, but these details are left to reader.)
For the COMSOL Multiphysics implementation, the displacements are found via a laser scanner, which only considers the axial displacement, whereas in a simulation software setup, the user also has access to the radial and normal displacements, which can lead to more accurate results. (In the present work, the simulation software COMSOL Multiphysics has been used throughout.)
Figure 3 shows how a simple total displacement can be decomposed into in-phase, anti-phase, and quadrature displacements.
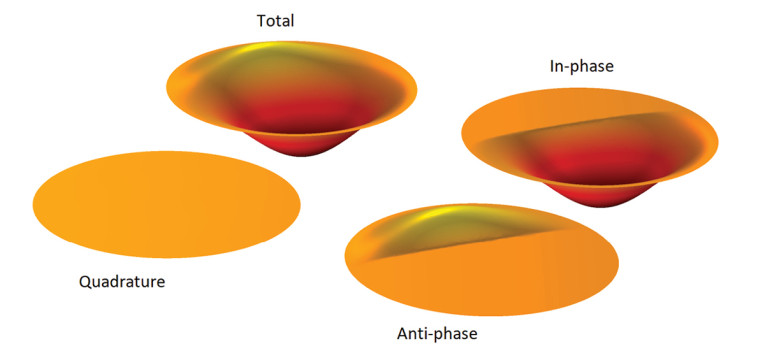
On the surface the displacement only has two phases — “inward” and “outward” — and so the bigger of the two sections will be the in-phase component driving the pressure, and the smaller section will be in anti-phase, and the quadrature component will be zero.
While the total displacement stays the same, the decomposition will vary depending on the microphone point in question as individual distances to the surface will vary accordingly, and so very different results can be seen off-axis and in the near-field.
For a more practical case, I have used an example from one of my clients, Charalampos Ferekidis, which is shown with his permission. Figure 4 shows the before (a) and after (b) sound pressure level for an initial driver and the subsequently modified driver. A dip was seen at 1kHz, and its origin was unclear.
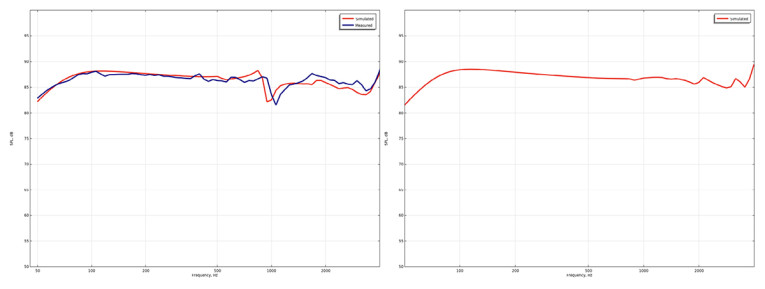
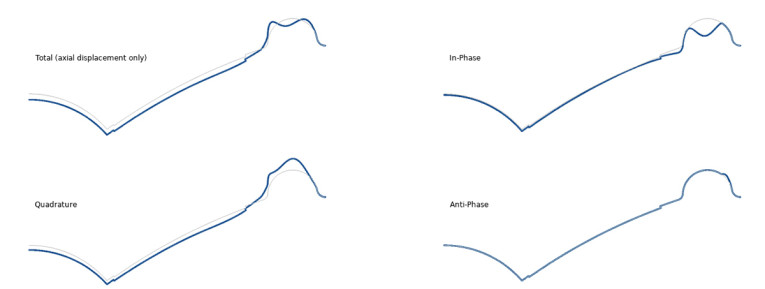
A phase decomposition analysis revealed the surround as the culprit, as its contribution was mainly in-phase, meaning driving the resulting sound pressure at that frequency, while the remaining displacement was largely quadrature, and so not adding to the pressure (Figure 5). Essentially, the driver is less efficient at radiating sound, since the effective area of radiation was located near the surround.
Other very interesting results can fall out of phase decomposition, and once it is implemented, it will typically be used extensively. The additional components such as Accumulated Acceleration Level (AAL) used within the Klippel environment can also be calculated within COMSOL Multiphysics, and typically with a higher spatial resolution in the simulation setup.
Axial-Symmetrical Decomposition
The axial-symmetrical decomposition is slightly more straightforward when it comes to how it works, but not straightforward to implement. I recently discussed this implementation in the blog post that I wrote for Acculution [6]. This decomposition does not rely on knowing the sound pressure at all, as it works directly on the total displacement alone. The split into components now is between a radial (or more accurately “meridional,” but we will stick to “radial” going forward) component and a circumferential component, both to be calculated for each frequency of interest.
The radial component has symmetry around the circumference, and so for example pistonic motion would fall into this category, as would any displacement that can be described as a variation along the radius which is then swept around the axis. The circumferential component is then any part of the total displacement that cannot be described this way. This could stem from modes or asymmetries in the setup. The equation for the radial component is:
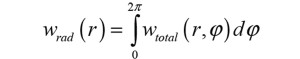
with r being the radius and φ being the circumferential angle. For each r on a continuum, a line integration is carried out along the associated circumferential line, and the resulting displacement varies along the radius only. Knowing this along with the total displacement, the circumferential component can be found as the difference between the two:
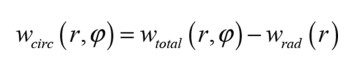
Concluding Remarks
It has been demonstrated how a total displacement on a cone surface can be decomposed into different components directly in the simulation software COMSOL Multiphysics, and how this can reveal some of the underlying mechanisms of the driver. The phase decomposition decomposes relative to a complex sound pressure, and certain aspects about limitations of the Rayleigh integral have not been touched upon here but can be found in that AES paper that I co-wrote with Skov [5].
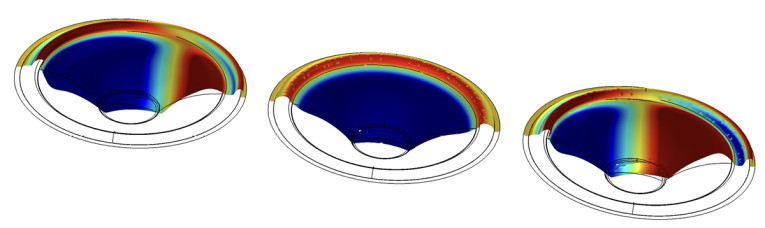
Another consideration is whether to use axial or normal displacements for non-flat surfaces, and that will be discussed in an upcoming publication with Charalampos Ferekidis. The axial-symmetrical decomposition technique decomposes directly on the complex surface displacement but is arguably more difficult to implement.
As the decomposition techniques shown here only consider the surface displacement, whatever is happening behind the driver (spider behavior, acoustic cavity modes) is seemingly not included in the decomposition. But in fact, it is, in the sense that if these effects affect the surface displacement, the decomposition will change accordingly.
Other decomposition techniques such as modal can also be carried out, and it is up to the engineer to figure out which approach will reveal the most insight for the case at hand. In future articles we may look at these alternatives. aX
References
[1] W. Klippel and J. Schlechter, "Measurement and Visualization of Loudspeaker Cone Vibration,” Klippel GmbH, Dresden, 01277, Germany and Faculty of Computer Science, University of Technology, Dresden, Germany.
[2] “Cone Vibration and Radiation Diagnostics,” Application Note to the Klippel R&D System, AN31, April 4, 2012.
[3] R. Christensen, “Phase Decomposition Analysis of Loudspeaker Vibrations,” Dynaudio A/S, COMSOL Blog, April 21, 2015
[4] R. Christensen, “Phase Decomposition for Loudspeaker Analysis,” GN Resound A/S and Dynaudio A/S, 2016 COMSOL Conference in Munich
[5] U. Skov and R. Christensen, “An Investigation of Loudspeaker Simulation Efficiency and Accuracy using A Conventional Model, A Near-To-Far-Field Transformation and The Rayleigh Integral,” 136th Audio Engineering Society (AES) Conference, Berlin, Germany, 2014.
[6] R. Christensen, “Axial Symmetrical Decomposition… In COMSOL Multiphysics,” Acculution Blog Post #036, August 29, 2021, www.acculution.com/single-post/axial-symmetrical-decomposition-in-comsol-multiphysics.
This article was originally published in audioXpress, January 2023