Why Another Preamp?
My reason for designing this preamp (Photo 1) is quite simple: I wanted to have a top-quality preamp without paying megabucks for a Levinson or Accuphase unit. It is up to you to decide whether or not I have succeeded in achieving the same quality. These were my design goals and decisions:
- Input switching. My hi-fi setup at home is fairly simple. I use one turntable, a compact disk player and one tuner in my permanent installation. Occasionally, I add a tape machine to this. Consequently, one phono input, two line inputs and a tape monitor input are all I need in a preamp. This should not, however, prevent you from adding several more inputs and tape features if you need them.
- Tone controls. I never use tone controls because they usually do not provide the required frequency range and boost/ cut. Theoretically, I am not against tone controls, and if there is sufficient interest, I will be more than happy to suggest a professional one.
- Circuit design. If I am a minimalist in terms of switching and other features, it certainly does not apply to circuit design. The circuitry is the heart of the amplifier, and I try to avoid compromises there. One important decision based on this philosophy was to use discrete circuitry instead of the more convenient integrated circuit (IC) op amps. I believe that a well-designed discrete amplifier produces better sound than one with op amps. I have drawn freely on previous experience (mine and others) in the audio field and in other electronics disciplines, notably instrumentation. I hope I have given credit where it is due.
- Mechanical components. Although not claiming to hear a difference between silver and gold contacts, I prefer the gold ones because of reliability. I want my preamp to work and sound the same three years from now, and I think only goldplated connectors and switches guarantee this.

RIAA Design Considerations
The two most important considerations when designing RIAA amps are dynamic range and RIAA accuracy. The dynamic range is limited on one side by the maximum input level it can accept without overloading the amplifier. The other limiting factor is the input noise of the RIAA stage. The range of input signals we can amplify lies between these two limits. Optimizing the dynamic range of an RIAA amplifier (or any amplifier, for that matter) means getting as much overload capability and as low noise as possible. Generally, you can increase the overload margin or upper limit by two means: operating the amplifier at very high supply voltages and keeping the gain as low as possible. When using IC op amps, the supply rails are automatically limited to approximately ± 15V because this is the maximum voltage the IC can handle. This limits the maximum output swing to around 7V RMS. Discrete designs have practically no supply voltage limit. Indeed, some manufacturers use ± 45V and ± 90V on the RIAA amp. 1 Tube preamps use even higher voltages.
We cannot do much about the gain because it is dictated by the sensitivity of the cartridge used. For movingmagnet cartridges, 34dB (or SO times) seems to be a standard. This will produce a O.SV output with a lOmV input. Assuming an IC-based RIAA amp with a maximum output of 7V RMS, the amp will accept an input voltage of 140m V maximum, which corresponds to an overload margin of 23dB. Figure 1 shows a level diagram for such an amplifier. With an input noise of around lμV, which is typical for op amps, you will have a dynamic range of 103dB for this RIAA amp.
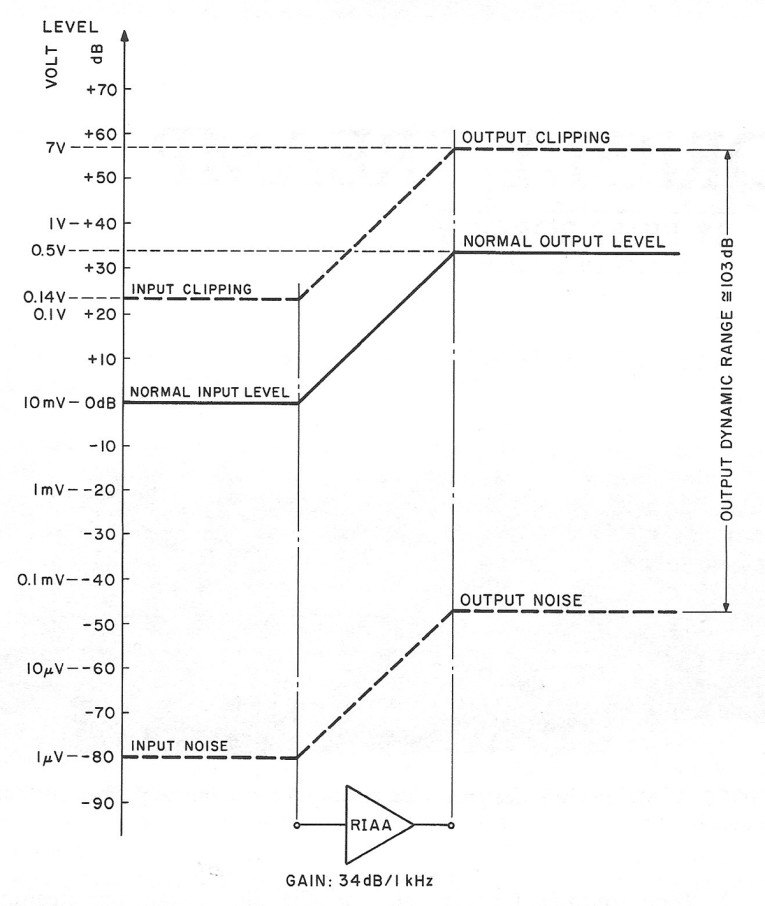
Up to now, I have considered signal levels at only lkHz. Due to the RIAA characteristics, the gain varies considerably at different frequencies. Compared to lkHz, the gain at 20Hz is almost 20dB higher, and at 20kHz it is approximately 20dB lower. Again assuming a lkHz gain of 34dB, we have to cope with a gain range of 14 to 54dB through the audio band. At 20Hz, where the gain is 54dB (or 500 times), the IC amp will accept only 7V /500, which equals 14mV; at 20kHz, where the gain drops to 14dB (5 times), the input overload is 1.4V. These numbers are based on the noninverting, single-op-amp RIAA stages most often used in preamps (Fig. 2). They are also theoretical numbers. Practical circuits with different op amps and feedback circuits might offer slightly better or slightly worse specifications.
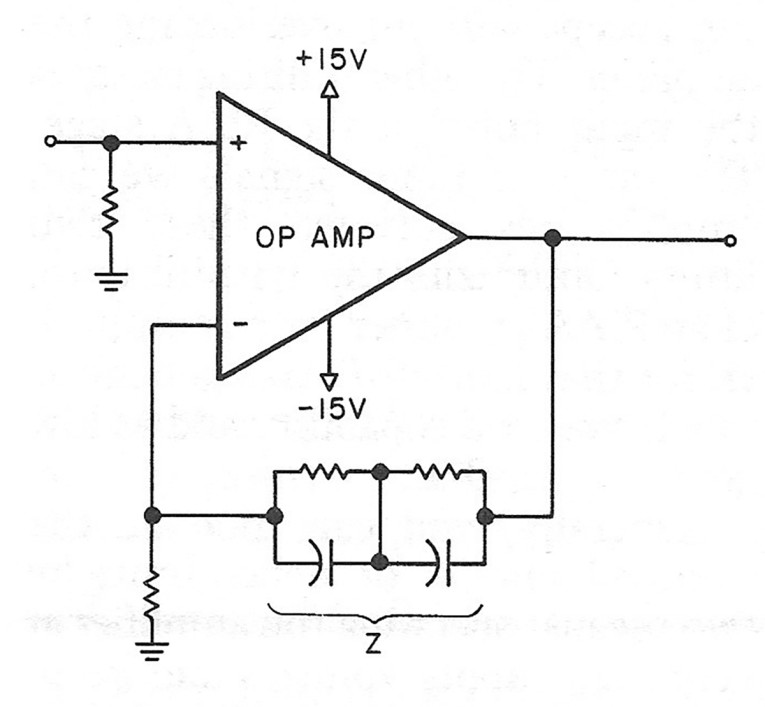
The single-stage RIAA amp shown in Fig. 2 has several disadvantages. The feedback network, which provides the RIAA correction, has a varying impedance with frequency. This impedance is lowest at high frequencies, which puts a very heavy load on the amp in the 10 to 20kHz range. Also, because the configuration is noninverting, the gain will flatten out at 1 (or OdB) even if you reduce the impedance of the feedback network to zero. This tends to give an equalization error around 20kHz. We have another problem at low frequencies, where the gain is very high, flattening out at around 54dB below 20Hz. To avoid equalization error, the open-loop gain of the amplifier must be significantly higher than the 54dB closed-loop gain. Traditionally, this was the biggest problem with early transistor RIAA amplifiers. With today's high-gain op amps, this problem is significantly reduced.
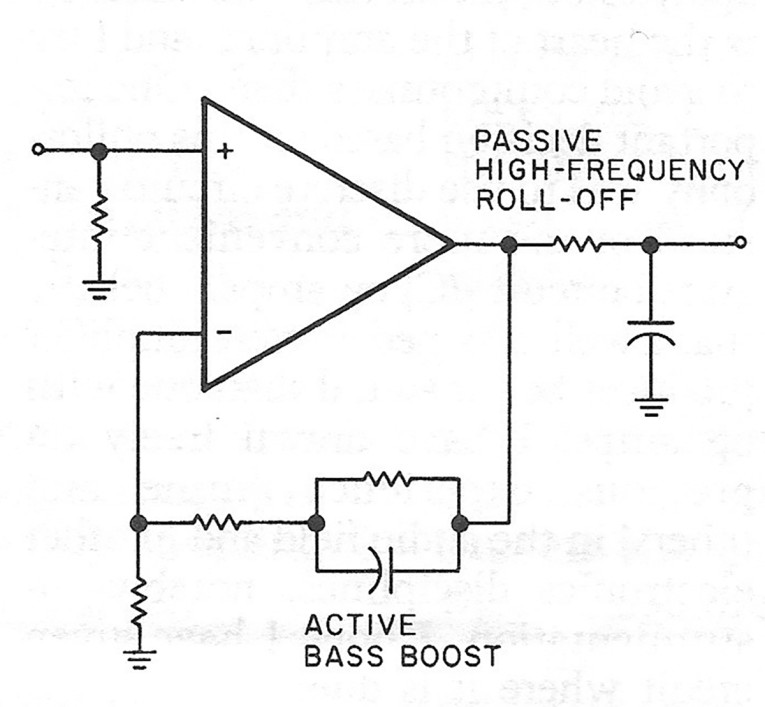
It is quite difficult to design a very accurate RlAA stage using the configuration of Fig. 2. Fortunately, we can solve two of the problems by removing the 75μ,sec roll-off from the feedback network and replacing it with a passive one as shown in Fig. 3. 2 This circuit removes the burden of low-impedance load at high frequencies and is inherently easier to calculate than the circuit in Fig. 2. The amplifier's open-loop requirement will remain the same as that of Fig. 2, but it introduces a problem of its own. Because of the passive rolloff, it reduces the overload margin at high frequencies. Also, you must consider any load on the output (volume control, tape recorder inputs, and so on) when calculating the 75μ,sec roll-off.
In the past few years, more and more high-end preamps have used a two-amplifier topology for RIAA. You might remember Dick Marsh's circuit from TAA 3/80 (p. 18) in which he used an all-passive RlAA equalization between two gain stages. Walt Jung reported the same approach at the Audio Engineering Society's 67th Convention. 3 Figure 4 shows such a two-stage, passively equalized RlAA amp.
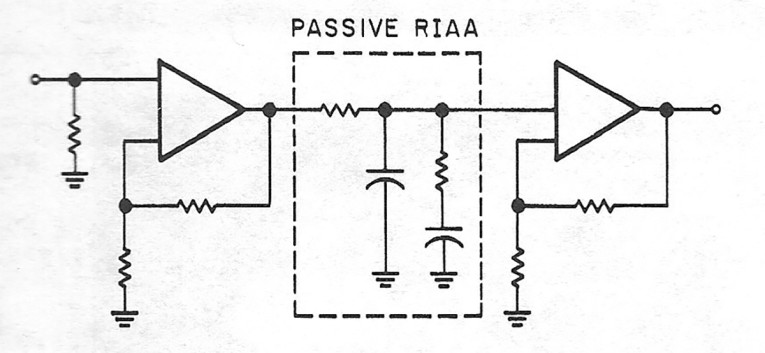
The all-passive approach solves the problem of high-frequency loading, but introduces some new ones. The most important consideration is the choice of gain distribution between the two stages. Low gain in the first stage and high gain in the second eliminates overload, but it means a very low input signal for the second stage, and this might create noise problems. The opposite is good for noise but bad for overload. According to Jung, optimum gain distribution is about 28dB in the input stage and 32dB in the second stage. Marsh opted for a lower gain in both stages of his T AA design.
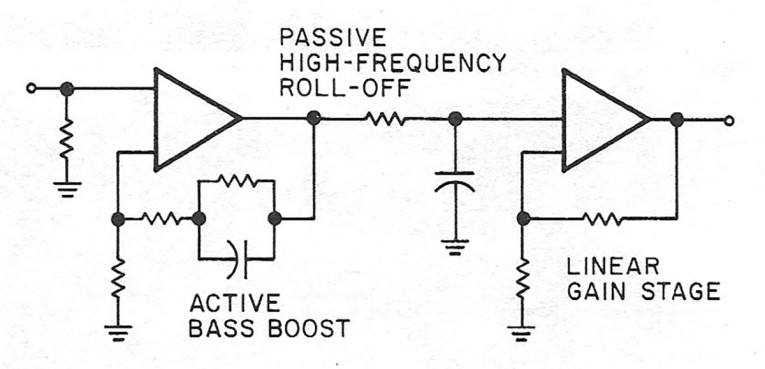
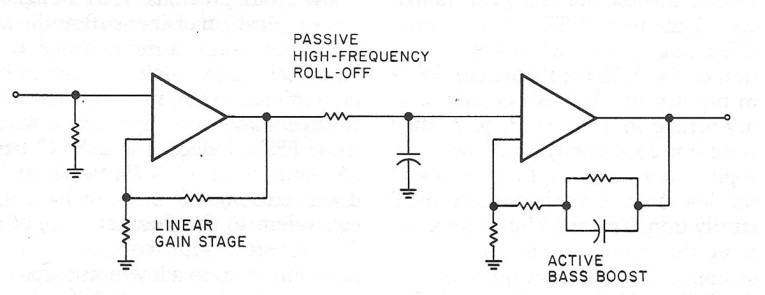
A different approach, combining the advantages of the circuits in Figs. 3 and 4"is shown in Fig. 5. Also a twoamplifier topology, it retains the passive high-frequency roll-off, but the bass boost is in the feedback loop. The advantage of this circuit is the lower gain required by both amplifiers, which lets you use gain blocks with low open-loop gain. Naturally, the bass boost does not have to be in the input stage. In fact, it is an advantage to put it in the second stage, as Jung suggests, 4 using • two instrumentation amplifiers in' a very elegant scheme with true differential input and gain adjustment in the input stage. I have chosen the same two-amplifier topology for my RlAA amp (Photo 2), but decided to stay with discrete circuitry (Fig. 6). The reason for this, in addition to the arguments presented above, is that I rate symmetrical, complementary design very high in terms of listenability. Unfortunately, none of the op amps on the market offers this kind of design.

The First Stage
As outlined in the previous section, I have chosen a linear amplifier as the first stage [Photo 3). This amp must have a very wide dynamic range (low noise and high overload capability), wide bandwidth and good linearity. In addition, the circuit should be symmetrical, using complementary design.

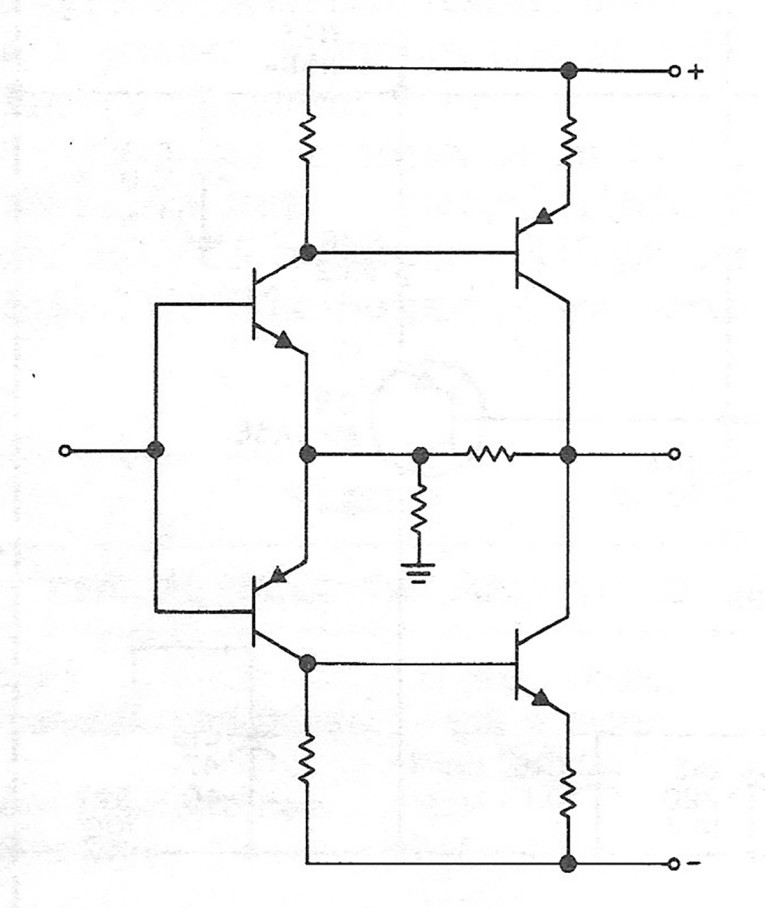
In selecting the basic topology, the low-noise requirement indicates that you should use single input instead of the more convenient, but inherently more noisy, differential input. Such a circuit is the cascaded complementary symmetrical amplifier shown in Fig. 7. This circuit was, to the best of my knowledge, invented by J. Davidson in 1965.5 You might remember this from Marsh's preamp;· he used it as a line stage. I spent considerable time on this topology from 1976 through 1978, adapting it to audio amps, instrumentation amps and pulse circuits. Part of the result of this research later went into the DH-101 preamp as the RlAA stage and as a pre-preamp. Because of two of the advantages of this circuit-low noise and high speed-I decided to use it for the first stage of the RlAA amp.
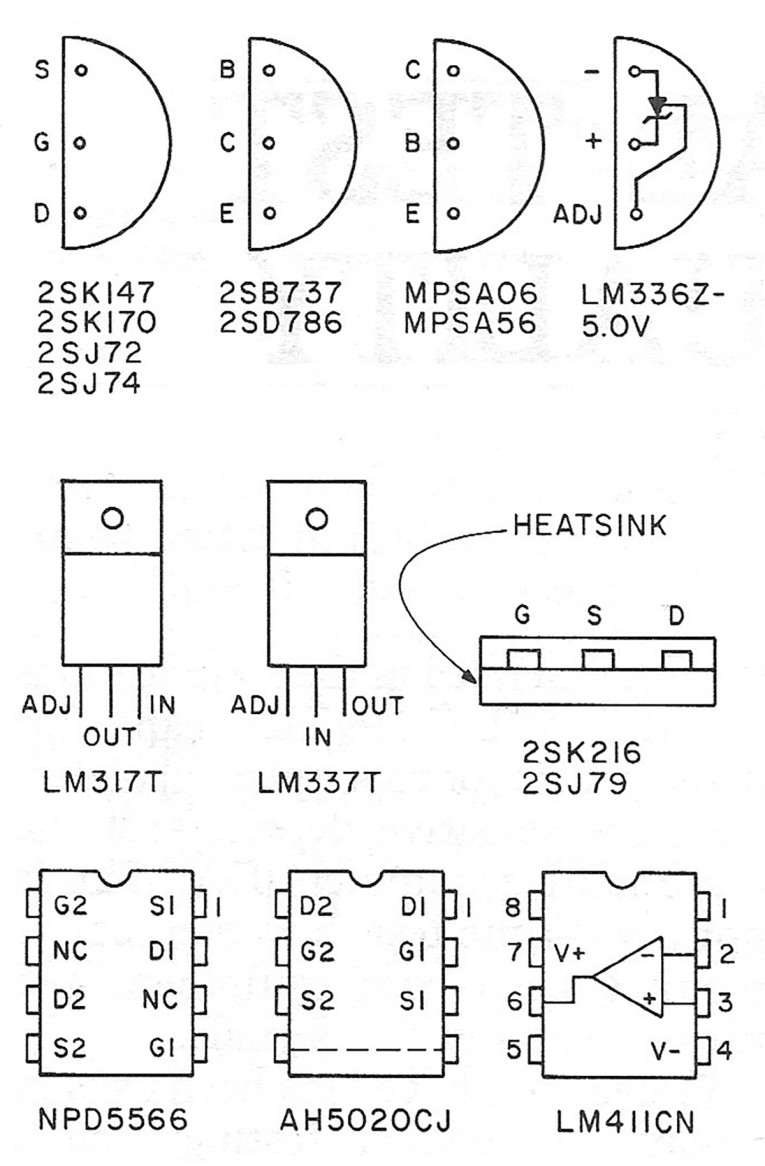
As you have probably noticed before, I have a preference for FETs in general and FET input stages in particular, so I wanted to replace the bipolar input transistors with JFETs, as shown in Fig. 8. As a matter of history, I tried to do this back in 1980, but could not find good enough complementary JFETs at that time. (That search resulted in the adaptation of the AH50:xx P-channel JFETs in my designs, but as I described in my article in TAA 5/83, p. 7, they were not good enough for low-noise applications.) In 1981, I learned about the low-noise complementary JFET family from Toshiba, 6 but it took me more than two years to get the first samples. The FETs in question are the 2SK147 N-channel and the 2SJ72 P-channel devices.
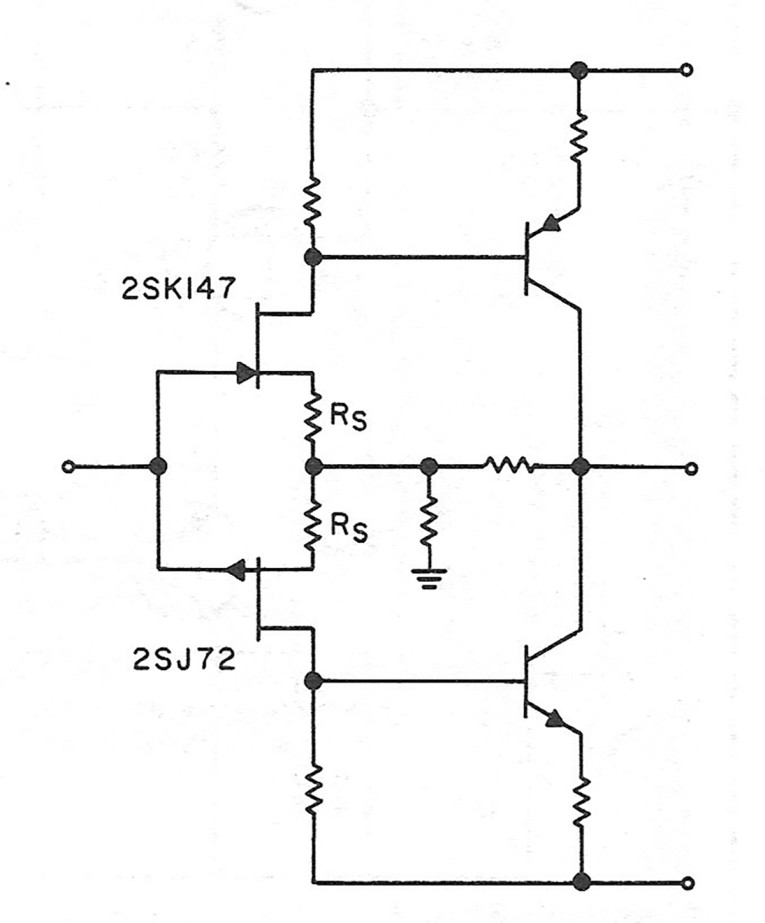
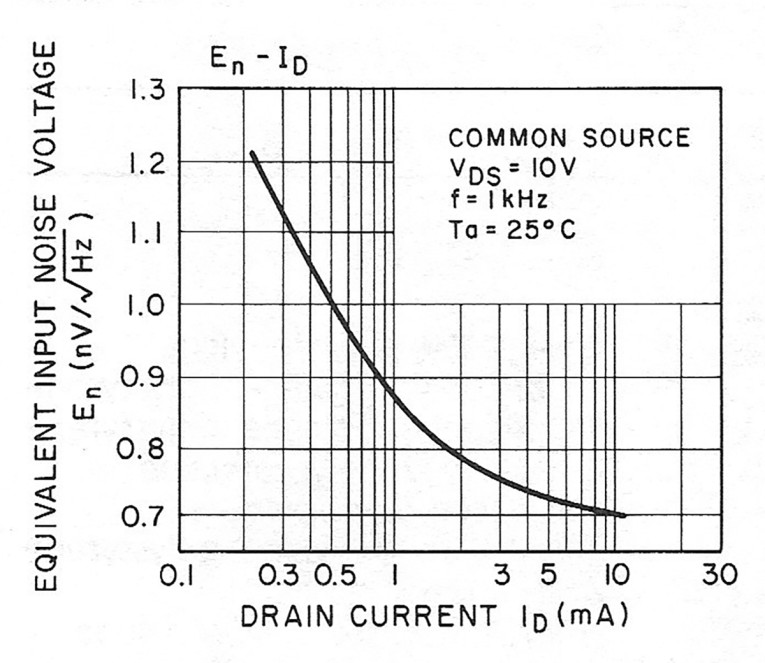
Apparently developed for low-noise audio applications, these FETs have a very high transconductance (gm). Typically, gm equals 40mmho at a drain current of 5mA. This is significantly higher than "normal" JFETs. The 2N5565, which I am sure you know from previous T AA designs, has a typical gm of about lOmmho at the same drain current. Since the equivalent input noise is inversely proportional to gm, it is quite natural to expect very low input noise with these FETs. Indeed, the 2SK147 has an input noise of 0.75nV/.}Hz at a drain current of 2mA, which is equivalent to the thermal noise of a 350 resistor. This compares quite favorably even to a low-noise bipolar transistor such as the LM394, which has an equivalent spreading base resistance of 400.
Unfortunately, you do not get anything for nothing, and in this case, you have to pay with a fairly high gate-to-source capacitance (Cgs). Cgs equals 60pF for the 2SK147 and 130pF for the 2SJ72. Worse yet, the feedback capacitance is also quite high-15pF for the N-channel and 55pF for the P-channel. When used in a normal common-source circuit, these FETs have a very high input capacitance because of the Miller effect. (The phenomenon by which an effective feedback path between the input and output of an electronic device is provided by the capacitance between specified electrodes. This can affect the total input impedance, which results in the total dynamic input capacitance being always equal to or greater than the sum of the static electrode capacitances.) You must take special precautions to avoid this in the final circuit. The simplified bipolar circuit in Fig. 7 does not show the necessary biasing for the input transistors. If you use JFETs that are normally "on," theoretically no biasing is needed. In a practical amplifier, however, you must reduce the rather large variation of Inss (saturation drain current measured with Vas = OJ. In the case of the 2SK147 /2SJ72, Inss equals 5 to 30mA.
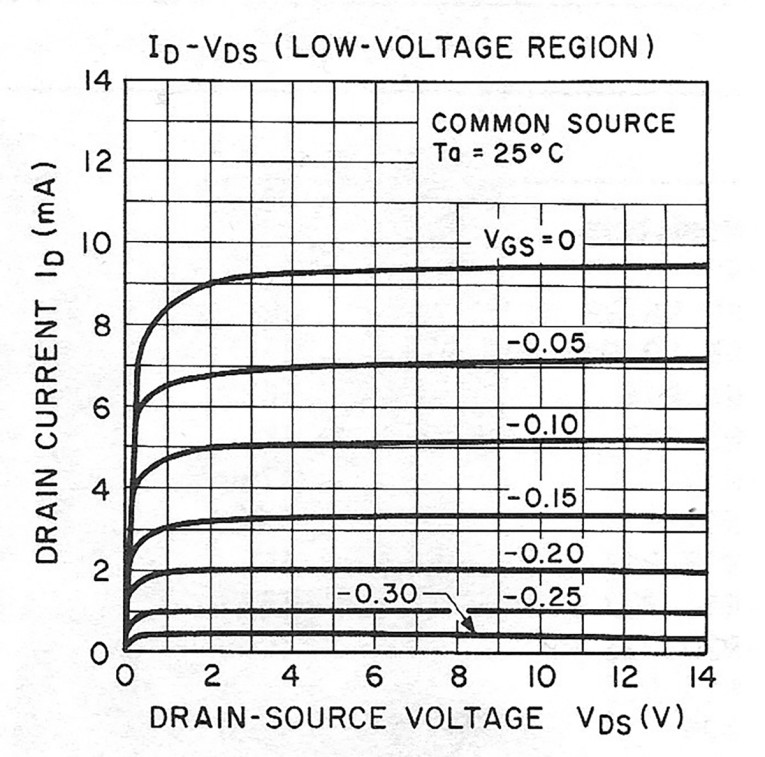
The FETs are available in three Inss groups from Toshiba: GR:5- lOmA, BL:8-16mA and V:14-30mA For optimum noise in this application, the FETs should be operated at In (actual drain current) greater than 2mA (Fig. 9). I have chosen to operate them at around SmA, which further improves noise performance and also increases gm. To stabilize the drain current at SmA, I inserted a resistor (Rs) in the source, as shown in Fig. 8. To select this resistor, you must look at the In-Vns (drain-source voltage) characteristics. Figure 10 shows typical characteristics for the 2SK14 7. You can read the gate-source voltage (Vas) off this figure: for an In of SmA, you need a Vas of approximately 0.lV. Therefore, Rs will be determined as follows:
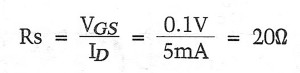
Ideally, the N and P-channel FETs should come from the same Inss group, and if possible, only the lowest two Inss groups should be used. If you get different Inss groups, you can still use them, but make some measurements to ensure proper operation. When supply voltage is applied, measure the voltage drop across the drain resistors. It should be about 2.8V. If it is more than 20 percent off (less than 2.2V or more than 3.3V), you must adjust the source resistors. When the voltage drop is too high, increase the source resistors; when it is too low, decrease them. Unfortunately, I cannot give you the correct Rsvalues for all combinations of Inss, so you must do some experimenting yourself. If this is beyond your resources, I suggest you buy this module fully assembled and tested from Old Colony.
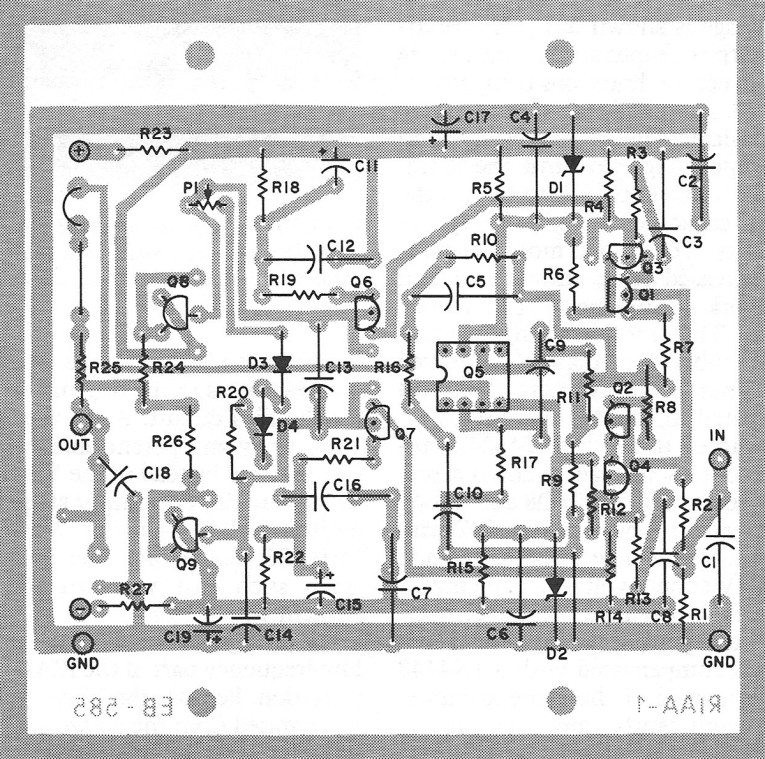
Figure 11 shows the complete schematic of the input stage. Because the FETs have negligible gate current, the cartridge is DC-connected to the input. Cl is the loading capacitor for the cartridge and should be selected according to the manufacturer's specifications. The amplifier's input capacitance is approximately 60pF, which should be deducted from the recommended value. You may solder Cl on the board. Ql and Q2 make up the input stage, cascaded by Q3 and Q4.
I have three reasons for using a cascaded input stage. First, for optimum noise, the FETs should be operated at less than a lSV drainsource voltage, according to the Toshiba data sheet. By biasing the cascade stage at lSV, the drain-source voltage will be limited to approximately 14.4V. Second, as mentioned before, the FETs have a very high input capacitance because of the Miller effect. Using a cascade configuration reduces this significantly. Finally, the cascade configuration is inherently more linear than the single, common- source stage. You need a ± lSV supply for the servo amplifier anyway, so adding the cascade is easy. The lSV bias voltage is taken directly from the lSV zeners.
The second stage of the amplifier consists of Q6 and Q7, which are normal common-emitter stages with partially decoupled emitter resistors. Rl9 and R21 introduce local feedback to improve linearity. Connect a highquality film capacitor in parallel with the electrolytic decoupling capacitor. Q6 and Q7 (and Q3/Q4) are special low-noise transistors from ROHM. Best known on the market for the lowest spreading base resistance, they offer extremely low noise with very low source impedances. Consequently, they are often used in pre-pre amps. Other transistors could.do the job from the overall noise point of view, but none offers the low flicker noise and the same linearity. One of the more important features of the preamp described here is the excellent low-level resolution. I attribute this, at least partially, to the input FETs and the ROHM low-noise transistors.
The output stage is an emitter follower, using the widely known MPSA06/MPSA56 general-purpose bipolar transistors. The bias network consists of Pl, D3, D4 and R20. Pl is used to adjust the quiescent current by measuring the voltage across the two emitter resistors. Set it to 1 V, which corresponds to approximately lSrnA. Put a small snap-on heatsink on these devices, as they tend to be hot. The layout is such that you can use other devices, including the Hitachi 2SK216/2SJ79 MOSFETs. In this case, you can experiment with the quiescent current to get the best sound. You do not need D3 and D4 with the MOSFETs, and you should change Pl to 5000 to get the necessary adjustment range.
Feedback resistors R9 and RIO set the gain of the first stage to approximately 11 times (20.SdB). I selected resistor values to produce as low noise as possible with the given drive capability of the output stage.
R25 and C18 provide the 75μsec roll-off for the RIAA equalization. In selecting the value of R25, take into account the output impedance of the first stage and the input impedance of the second stage. R25 should be a 1 percent metal film resistor and C18 a 1 percent polypropylene or polystyrene capacitor.
The servo amplifier is an LF411 BIFET op amp. I selected Rl6/C10 and Rl7/C9 to give a -3dB of less than lHz. The output of the servo amp is connected to the feedback point through a 5.6kn resistor. The servo is capable of compensating an input offset of ± 100m V.
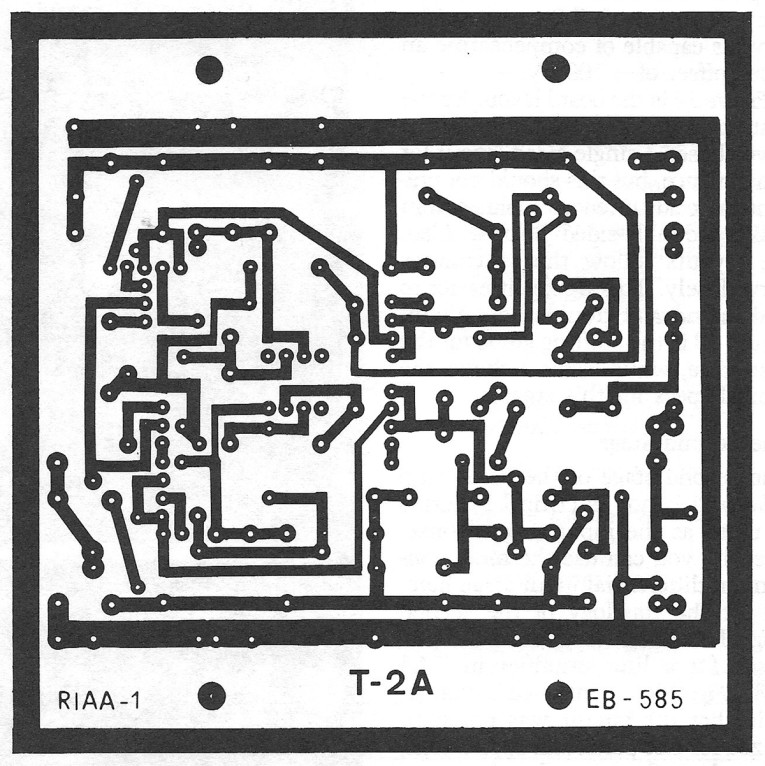
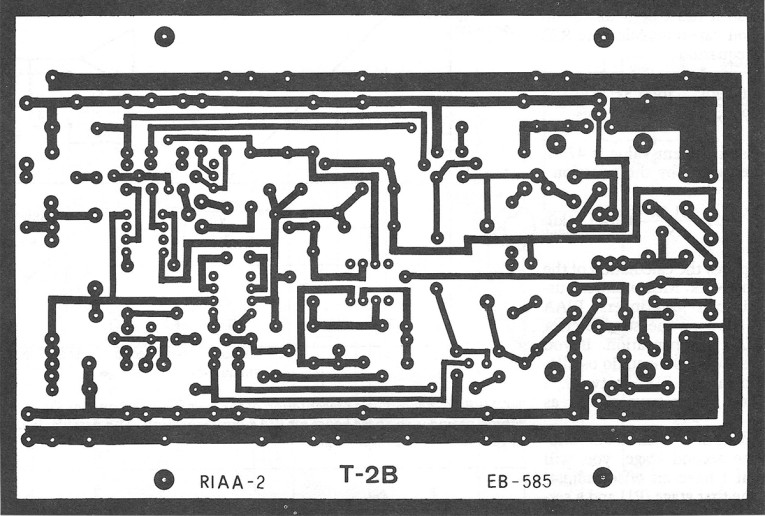
Figure 12 is the board layout for the first stage of the RIAA amplifier. I have chosen a single-sided layout for convenience, but this should not prevent more advanced audiophiles from making double-sided boards. Also, the layouts follow the schematics very closely. This makes it easier to understand and troubleshoot them. Figure 13 is the stuffing guide for the first stage, while Table 1 shows the typical specs for this stage.
The Second Stage
The second stage of the RIAA amp (Photo 3) is not as critical in terms of noise as the input stage. Consequently, you can use the more convenient differential input stage here. As for the topology of the second stage, I have chosen the same as I proposed for a line amplifier in T AA 5/83 {Fig. 14). I mentioned in that article that the circuit was not optimized for one particular application, but it showed very good performance in speed and linearity. I have now optimized it for the second stage of the RIAA amp and my line amp.
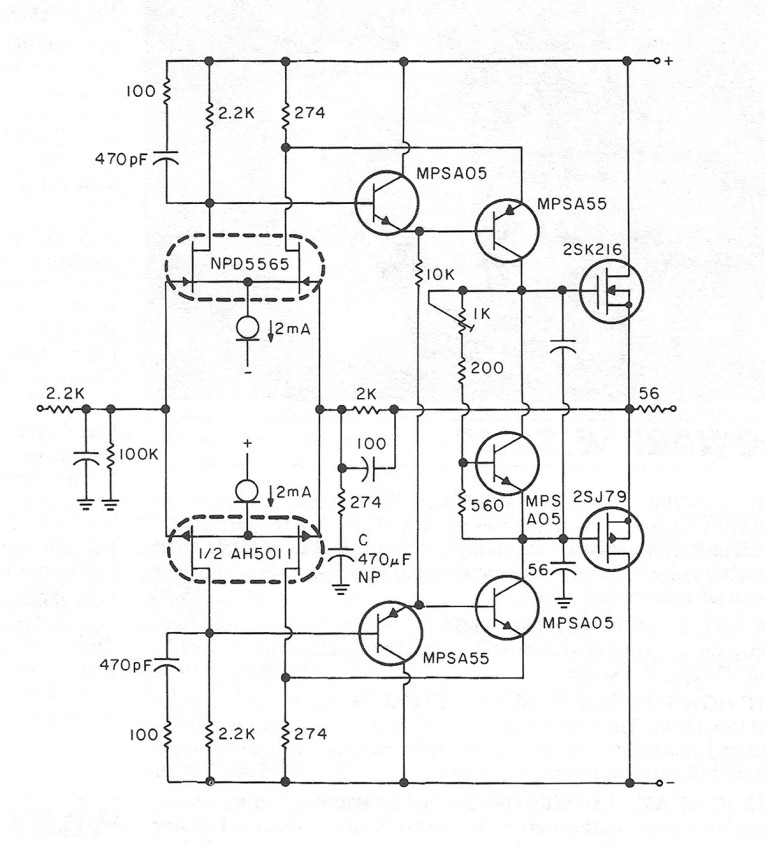
The complete schematic of the second stage is shown in Fig. 15. Starting with the input stage, I havemade two major modifications compared to Fig. 14. First, I added a cascade stage for basically the same reasons as in the input stage: to iimit the drainsource voltage to 15V, to reduce the input capacitance and to improve linearity. The second modification is an increased drain current: Ql and Q2 work at SmA per FET to reduce noise. This modification, together with on-board regulators, improved the input noise by more than 6dB compared to the original circuit.
I wanted to use the LM334Z current sources instead of the discrete ones consisting of Q7 /Q8 and associated circuitry, but the LM334Z cannot handle the power dissipation and the 24V supply voltage. The current sources shown have a partial temperature compensation: the transistor's VnE is compensated with a 1N4148 diode instead of the more accurate, but significantly more expensive, dual-transistor approach I used in the DC-100 power amp. The reason I can get away with this is that I added a servo circuit to the amplifier.
The second stage of the amplifier is the same as in the original, except for the bias circuit. As in the input stage, I rely on a potentiometer to adjust the bias instead of the VnE multiplier circuit. The output stage is an emitter follower using MPSA06/ MPSA56 transistors. The layout is again such that you can add the Hitachi MOSFETs.
R20, R22, R23 and Cf make up the low-frequency part of the RIAA compensation. Because the 75μsec roll-off is separated from the active compensation, it is easy to calculate this feedback network. 2 To make the calculation easier to understand, the lowfrequency part of the RIAA frequency response is shown in Fig. 16. The resistor designations are the same as the ones in Fig. 15.
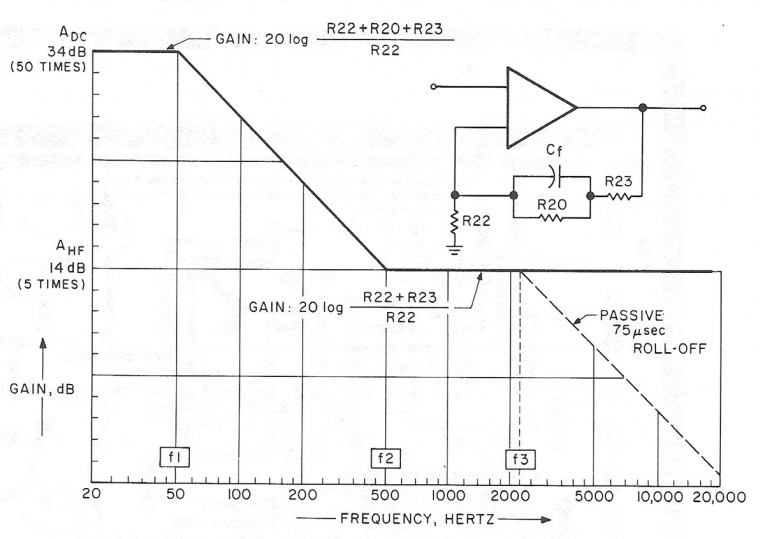
The fl = SOHz breakpoint is given by the equation
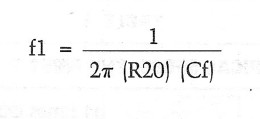
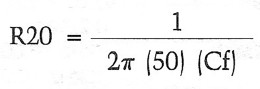
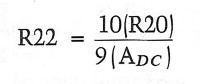
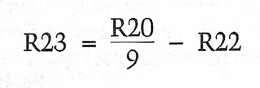
Let's go through the calculation of the network I used. In selecting the capacitor Cf, you must consider the overall impedance of the feedback network. For low noise, the impedance should be as low as possible. There is, however, a limit to how low you can go because the amplifier has to be able to drive it. Also, the lower the impedance of the network, the larger the value of the capacitor. I wanted to use precision polypropylene or polystyrene capacitors, so I had to look at what was available on the market with, say, 1 percent tolerance. Values up to 0.lμF are easy to find, but higher values normally require paralleling of smaller ones.
I calculated the feedback network for capacitor values between 0. lμF and 0.33μF, finally settling on 0.147μF, which is 0.1 in parallel with 0.047. (I also used 0.047 for the 75μsec roll-off in the first stage.) R20 can be found with the equation
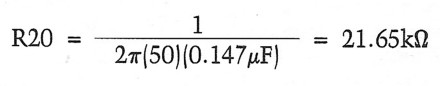
The closest value in 1 percent metal film is 21.Skn, so I used this in the amplifier. To be able to calculate R22, you must know the gain at very low frequencies. If you select a total gain of 34dB for the RIAA amplifier and the first-stage gain is 20dB as shown earlier, then the second-stage gain has to be 14dB (or 5 times) above lkHz (AHF). Ave is equal to 10 times AHF (Fig. 14), so it must be 34dB (or 50 times). You can now calculate R22 from the equation
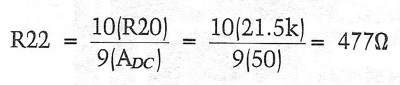
The closest 1 percent value is 475. R23 is then given by the equation
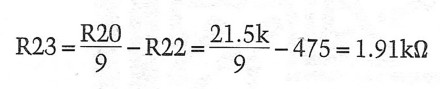
Continuing now with the description of the second stage, you will notice that I have an offset adjustment in the first stage (Pl) and a servo amplifier. This is a bit of overkill: you do not really have to adjust the offset if you have a servo, but I prefer doing that just to know what the initial offset is. Also, while I cannot get rid of the servo (FETs have a significantly worse temperature behavior than bipolars), I want it to track temperature drift only, not initial offset. (The same arguments could also be applied to the first stage, but I did not want to put a trimpot there for noise and distortion reasons. Remember the extremely low-level signals we are amplifying in that stage.) Proper setup procedure, in case you choose to use both, is to adjust the output offset to zero before inserting Q9. If you do not use Pl (R12/R13 are then 220 each), simply insert Q9, and it will take care of the offset. Pl should be a cermet trimpot for low noise and good stability.
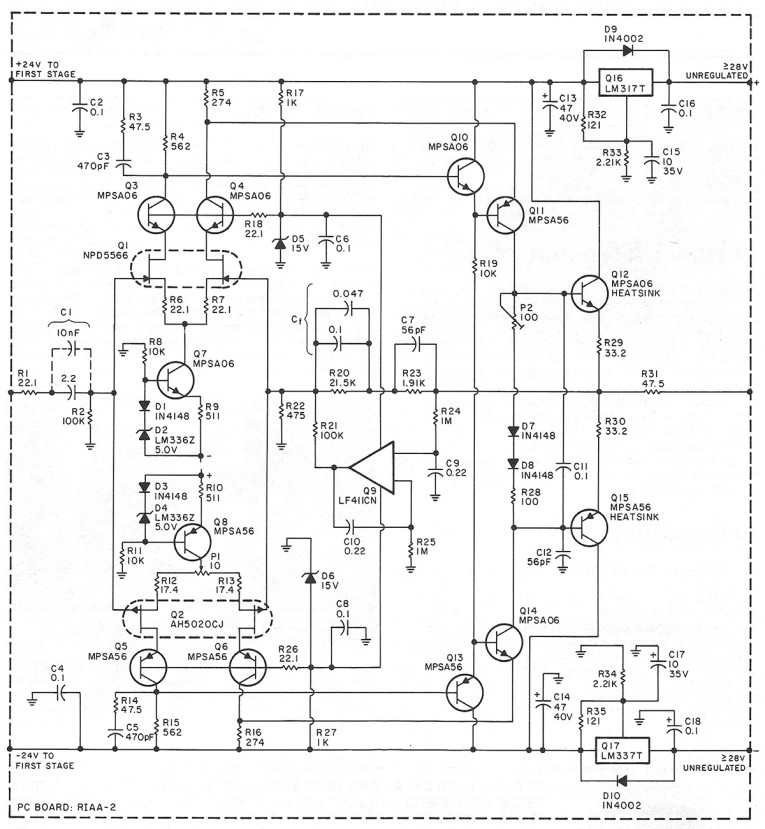
Q16/Ql 7 and associated components provide regulated ± 24V to the second stage of the RIAA amp and, through a further RC filter, approximately ± 22V to the first stage. I chose the LM317 /LM337 three-terminal regulators for these functions. I recommend all three capacitors shown in connection with the regulators: C16/C18 for stability reasons, C 15 / C 17 to improve ripple rejection and output impedance, and C13/C14 to improve load transient response.
C2/C4 are high-quality film capacitors, helping to improve high-frequency decoupling. In case of accidental shorting of the input to the regulators, output capacitors C13/ C14 will discharge into the output of the regulators. When C13/C14 are larger than 25μ,F, this discharge can cause damage to the regulators. Diodes D9/D10 prevent this damage. The regulators should be mounted with a heatsink, with thermal resistance of approximately 20°C/watt. I used a heatsink that can be soldered to the board, but you can adapt other heatsinks easily.
Although the LM317 /LM337 regulators have quite low output impedance up to lO0kHz (less than 0.20), there has been some discussion in T AA that this is not good enough for preamps. Without taking sides, I suggest that you make your own decision: if you think that you might gain in sonic quality by using a discrete regulator, do not hesitate to design one. You can simply leave out the regulators when you assemble the board and connect the supply lines to your own regulator.
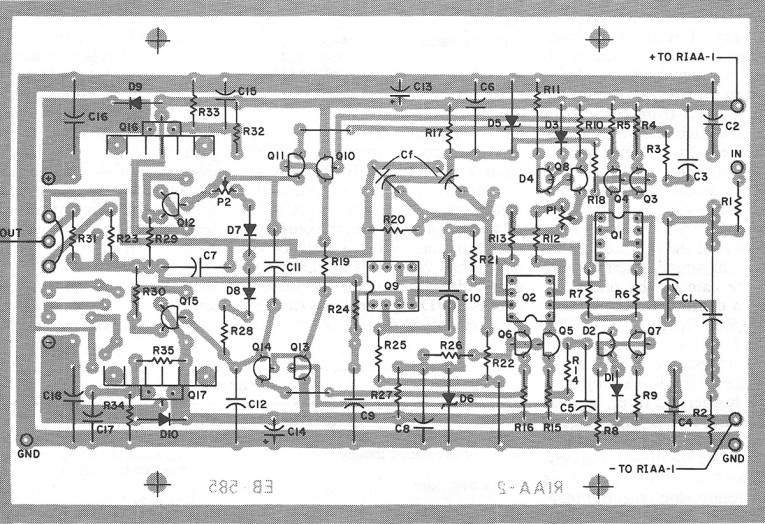
Figure 17 is the board layout for the second stage of the RIAA amplifier, and Fig. 18 is the stuffing guide. I used gold-plated sockets for Ql, Q2 and Q9; the other components are soldered directly to the board. Table 2 shows the typical specs for the second stage. Table 3 shows the typical specs for the complete RIM amplifier. Figure 19 shows the pin-outs for the devices used in my design.
References
l. Perreaux: SM2 preamp, Audio, July 1984.
2. Baxandall, P.J., "Letters to the Editor," JABS (Volume 29, Number 1/2), January /February 1981.
3. Jung, W.G., "Topology Considerations for RIM_Phono Preamplifiers,11 Preprint 1719, 67th Convention of the AES, October 31/November 3, 1980.
4. Jung, W.G., and S. Wurcer, "Instrumentation Amplifiers Solve Unusual Design Problems,"EDN, August 4, 1983.
5. Davidson, J.J., "Low Noise Transistorized TapePlaybackAmplifiers, 11 JABS (Volume 13, Number 1), January 1968.
6. Netzer, Y., "The Design of Low-Noise Amplifiers 1 11 Proceedings of the IEEE (Volume 69, Number 6), June 1981.
7. Lipshitz, Stanley P. and Walt Jung, "A High Accuracy Inverse RIAA Network," TAA 1/80, p. 22.
Read also Borbely RIAA Preamp With Tubes - A Project Remembered and Revisited
This article was originally published in The Audio Amateur Issue 4, 1985.





