His invention of the Helmholtz resonator, described in his book On the Sensations of Tone (which was first published in German in 1863) grew out of his interest in the physics of perception. Photo 2 shows an early lab model of the resonator mounted beside an electrically-driven tuning fork that acted as an acoustical continuous-wave source.

The actual resonator is the cylindrical object on the right side of the image shown in Photo 2. It comprises a hollow cylinder (wood, in this case, but it can be virtually any material) with a hole in one end. Physically, the springiness of the air in the cylinder resonates with the mass of air in the neck produced by the hole passing through the wall of the device. Even if the neck is very short (thin-walled end plate on the cylinder), the so-called “end effect” causes a certain amount of the air on the inside and outside of the hole to move more or less together. The interacting air mass and springiness behave as a simple spring-mass mechanical oscillator, responding strongly at one frequency, given by the equation:

Where c = the speed of sound, S = the area of the hole, l = the length of the hole (thickness of wall that the hole penetrates), and V0 = the volume of the cylinder.
The shape of the vessel enclosing the air is unimportant; only the volume of the enclosed air matters. A common example of a Helmholtz resonator is a soda bottle or cider jug (as in “a jug band”) with air being blown across the hole in the top. In this case, the resonance causes the air in the neck to move with high velocity at the frequency of resonance, creating a more-or-less single-frequency tone. Accidental Helmholtz resonance sometimes occurs when a single car window is partially or fully open, resulting in a loud sound, often called “wind throb.”
Early Helmholtz Resonators
Early applications of Helmholtz resonators predate von Helmholtz by many centuries. In ancient buildings from Greece to Scandinavia, urns or pots of various shapes were incorporated in the walls to boost or tame specific frequencies for acoustical benefit. In some cases, ashes have been found in the urns, presumably having been used as damping agents to increase the effective bandwidth of the resonator. Helmholtz resonators incorporating damping act as acoustical notch filters, removing acoustical energy at the resonance frequency. The Queen Elizabeth Hall in London has 2,300 Helmholtz resonators in boxes lining the walls to reduce bass predominance caused by the massive concrete walls.
Common Uses
One of the most common uses of Helmholtz resonators is as mufflers for internal combustion engines. The specific design of the resonator affects both the sound of the exhaust and the power delivered by the engine. The Chrysler V10 engine used in the Dodge Viper and in Ram trucks uses “Helmholtz Systems” in the air intake.
Another case of Helmholtz resonators being used to remove unwanted sound is the duct silencer in HVAC systems. The fans in these systems produce a lot of low-frequency noise that is most effectively removed by use of a resonating silencer.
Helmholtz resonators are essential components of many musical instruments. One of the primary radiating modes of a violin, viola, cello, string bass, guitar, or mandolin is the Helmholtz mode. The body of these instruments encloses the air that provides springiness, while the f-hole or sound hole is the opening.
Luthiers must control the dimensions of these openings carefully in order to tune the instrument for boosted output at the proper frequency. For example, most classical guitar resonances are tuned to the “B” one octave plus one semitone below middle “C,” which is a frequency of about 123 Hz. Too large a sound hole would make the resonance frequency too high, and the guitar would sound thin. Too small a sound hole would move the resonance lower, to where the guitar is a less effective radiator, making it sound less loud overall. Somewhere there is a “sweet spot,” which each luthier must choose when designing an instrument.
Other musical instruments employing Helmholtz resonators include the ocarina (or “sweet potato”) and the djembe drum. In the case of the ocarina, covering the holes reduces the total area of the “Helmholtz hole,” changing the frequency it produces (see Photo 3). The djembe has a long neck, giving it a low resonance and a deep tone (see Photo 4).


Controlling Sound Levels
Helmholtz resonators are also useful for controlling sound levels at modal frequencies in small listening rooms and studios (see Photo 5). In this application, the tuning frequency of the “bass trap” is chosen to eliminate the most problematic mode, and the damping is controlled in order to adjust the bandwidth of the resulting acoustic notch.

Because bass traps act locally, they can be located where modal peaks are greatest, thus having less effect on the listening locations where narrow-band attenuation is not needed. In this respect, they differ from electronic DSP notch filters, which remove energy fed to the speakers at specific frequencies, thus affecting the entire room equally.
As discussed in my June 2016 audioXpress article, “The Difficult and the Impossible in Acoustics,” Helmholtz resonators have been successfully used to provide low-frequency absorption in small, lightweight acoustic metamaterials. Yong Li and Badreddine Assouar have developed a metamaterial using the principle of tuned absorbers.[1] The device consists of a coiled chamber placed behind a perforated panel, as shown in Photo 6. The dimensions are: a = 100 mm, b = 1 mm, w = 12 mm, and d = 3.3 mm.
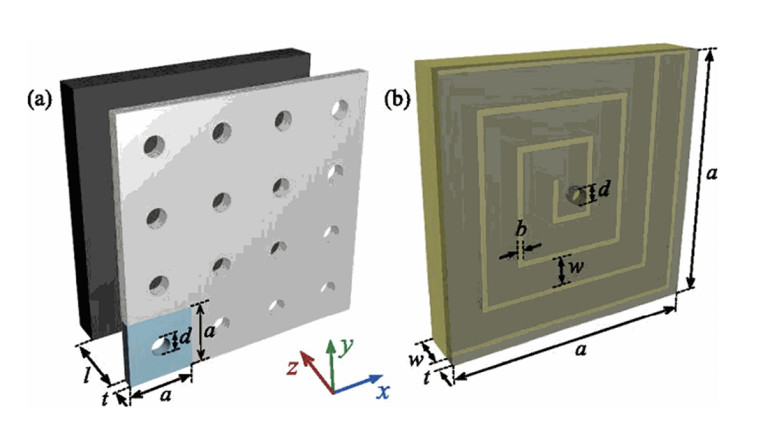
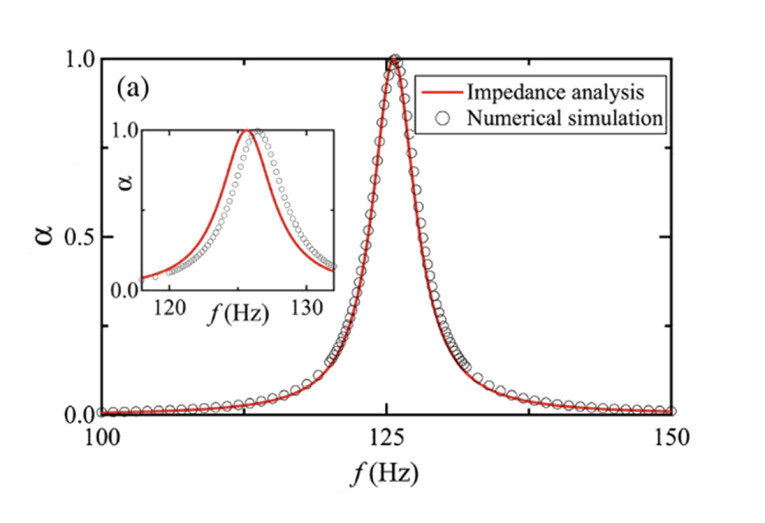
Figure 1 shows the variation of the absorption coefficient with frequency. As you can see, the Q is very high. The coefficient of absorption reaches 100% at the tuning frequency of 125.8 Hz. The total thickness of the system is 1/223 times the wavelength of the tuning frequency. Notice how this compares with 4” thick fiberglass (1/27 wavelength), which only has an absorption coefficient of 0.88 at 125 Hz.
Bass Reflex Speaker
In the 1940s, a speaker system design called the bass reflex speaker was introduced. The goal of the design was to improve the bass response of speaker systems without enlarging the cabinet any more than necessary. Before the 1970s, this design was used more by DIY builders than by commercial manufacturers because its operation was not well understood.
A pioneering paper by James Novak of Jensen, followed by other works by A. Neville Thiele, Richard Small, and others, brought the design of these systems onto a level with predictable engineering approaches. Along with the new popularity of these speakers came a name change: they were now called “vented” (sometimes “ported”) speakers, because “bass reflex” had become associated with the boomy sound that often resulted from poor design.
Figure 2 illustrates a vented speaker system. As you can see, the cabinet functions as the enclosure of a Helmholtz resonator, and a tubular port or vent acts as the hole. By controlling the enclosure volume, cross-sectional area of the vent, and vent length, the designer can control the “box frequency.”
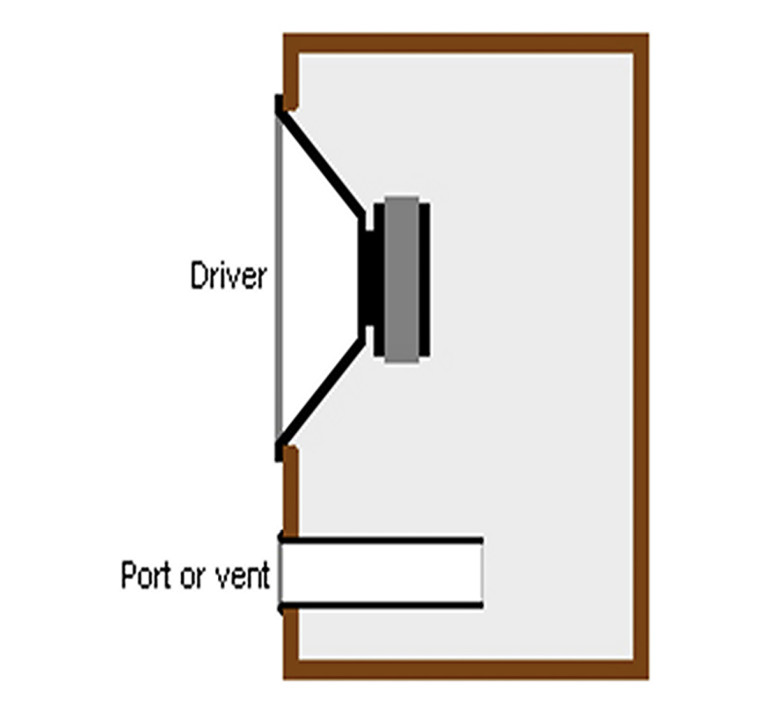
If this frequency is correctly coordinated with the electro-mechano-acoustical resonance frequencies and “Q’s” (quality factors) of the driver, predictable results can be obtained in the finished product. The detailed technical analyses provided by Novak, Thiele, Small, and others has been distilled into user-friendly form for both DIY-ers and professionals in Vance Dickason’s Loudspeaker Design Cookbook, 7th Edition.
The passive radiator speaker is a slightly different but conceptually similar design. It uses a diaphragm much like a speaker cone, but with no voice coil, instead of the moving air mass of the Helmholtz resonator. The passive radiator (often called a “drone cone” in years past) was introduced in 1954 by Harry Olson, John Preston, and Everrett May. The additional mechanical and acoustical complexity of the passive radiator compared to a vent port or simple vent allows some additional options for the speaker designer.
For those readers who have studied physics, this survey of Helmholtz resonator history, operating principles, and applications should provide verification of your physics teacher/professor’s emphasis on the importance of understanding the simple spring-mass oscillator! aX
Reference
[1] L. Yong and A. Badreddine, “Acoustic metasurface-based perfect absorber with deep subwavelength thickness,” Applied Physics Letter: 108, 063502 (2016),
http://dx.doi.org/10.1063/1.4941338.
Resources
V. Dickason, Loudspeaker Design Cookbook, 7th edition, December 2005, available via www.cc-webshop.com/Loudspeaker-Design-Cookbook-AA-BKAA068.htm.
H. Helmholtz, On the Sensations of Tone, 1863.
R. Honeycutt, “The Difficult and the Impossible in Acoustics,” audioXpress, June 2016.
H. Olson, J. Peston, and E May, “Recent Developments in Direct-Radiator High-Fidelity Loudspeakers,” Journal of the Audio Engineering Society (JAES), 2(4), 219.
This article was originally published in audioXpress, January 2017.