This article shows that in the digital domain, you can implement these “unrealizable” phase corrections in a very straightforward way, although there is still an approximation involved. Whereas Dennis Colin’s article is primarily concerned with phase corrections for the crossover, my focus here is on compensating for phase nonlinearities in the driver. Even if you are not attempting to construct a “linear phase” speaker system, nonlinear phase behavior can still make it difficult to smoothly blend together the responses of the different drivers in the system. This article illustrates the problem for the midrange driver in a three-way system, which will be crossed over to a woofer on the low end and a tweeter on the high-end.
The Problem
Figure 1 shows a portion of the measured impulse response of two Vifa P13WH midranges connected in series in an MTM arrangement. I obtained this data using the Virtual Crossover with an MLS sequence of order 15 (for information about the Virtual Crossover, visit www.acoustic-instruments.com). I took the measurement with the microphone on-axis and about 6′ from the drivers. In Fig.1, the vertical line shows where the measurement data was truncated before calculations were carried out in the frequency domain — i.e., the waveform to the right of the vertical line was assumed to be zero. This is done in an attempt to eliminate the effects of room reflections.
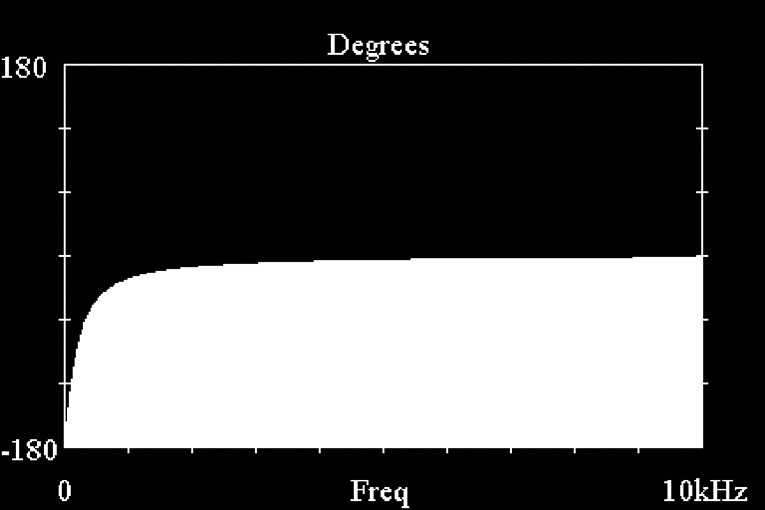
Figure 2 shows the phase response of the midrange drivers out to 10kHz, obtained from FFT (Fast Fourier Transform) calculation using the data from Fig.1. Interpreting phase response data can be tricky; I highly recommend the article by Bill Walso (3) if you need more information on the meaning of phase characteristics. For the purposes of this article, it is important to know that the delay of a frequency component increases as the slope of the phase versus frequency curve increases in the negative direction. Looking at the data in Fig.2, you can then see that a frequency component at, say, 500Hz is delayed in time more than a frequency component at 3kHz (the phase data in Fig.2 is plotted on a linear frequency scale).
In my case, the midranges are crossed over with the woofer at 500Hz and with the tweeter at 3kHz. From Fig.2 you can see that the slopes of the phase versus frequency characteristic are substantially different at these two crossover points. In Fig.2, the area in white extends from 250Hz to 1kHz, one octave below and above the intended crossover point with the woofer; this is the area I will concentrate on for phase correction.
To illustrate the problem that occurs, assume that the drivers are in time adjustment such that the phase response of the woofer stays around zero degrees in the vicinity of 500Hz, and likewise the tweeter phase response is near zero degrees around 3kHz. In that case the crossover between midrange and tweeter should be smooth, but due to the rapid phase variation of the midrange with respect to the woofer phase near 500Hz, there may be alternate cancellations and reinforcements in the combined responses of the midranges and woofer, depending upon the order of the crossover that is used. In particular, if a first order crossover is used, which is normally thought to be “transient perfect,” the result obtained will be far from ideal at the lower crossover. Not only will pulse wave forms not be preserved, but the overall magnitude of the response will not be constant.
Alternately, if the phase response of the woofer is aligned with that of the midranges in the crossover region, there will be an abrupt change in slope of the combined phase response of the system, again preventing faithful reproduction of transient waveforms. One way to address this problem is to use a phase correction network to extend the near-zero phase region of the midranges in Fig.2 to lower frequency, below the 500Hz crossover point with the woofer.
All-Pass Networks
In general, an all-pass network is a circuit or transfer function that alters only the phase of a signal, not its amplitude. For example, consider the following transfer function T(s) of complex frequency s:
T(s) = s-W0 / s+W0
where s = jw for the constant frequency case. Equation 1 describes a first-order all-pass network. Note that the magnitudes of the numerator and denominator in Equation 1 are always equal, so that the magnitude of any frequency component passing through this network is preserved. However, the phases of different frequency components are altered.

Figure 3 shows the phase for a transfer function of the type in Equation 1, where w0 = 2pf0 is the corner frequency of the all-pass network and the frequency where the phase shift is 90°. In Fig.3, f0 was chosen to be 200Hz, in anticipation of the corner frequency that will be required to compensate for the midrange phase response. Note from Fig.3 that the slope of the phase versus frequency starts out negative for low frequencies, but flattens out to near zero slope at higher frequencies. This means that the all-pass network delays low-frequency components relative to higher frequency ones.


Figure 4 shows the impulse response of the first-order all-pass network, for the case f0 = 200Hz. The impulse at t = 0 passes higher frequencies with no delay, whereas the “tail” of the impulse response produces varying delays for lower frequencies (in this figure, I started the plot at -1ms in order to clearly show the impulse at t = 0). There are different methods of realizing the first-order all-pass transfer function. Figure 5 shows a “constant resistance” implementation(1). In this circuit, provided that R, L, and C are selected according to the formulas in the figure, the network will appear as a constant resistance R at all frequencies at the vin port, and vout/vin will have the phase transformation as in Fig.3 (but this circuit gives an overall inversion, equivalent to adding 180° everywhere in Fig.3). Please see references 1 or 2 for op amp circuit implementations of all-pass networks.
I should mention that other all-pass networks are possible besides the one given in Equation 1; second-order and higher order implementations can be realized. However, in this article I will treat only the first-order case. Comparing the phase response of the first-order all-pass in Fig.3 with the midrange phase characteristic in Fig.2, you can see a big problem: the all-pass phase correction in Fig.3 goes the wrong way! What you want is to flatten the midrange phase down toward zero at lower frequencies, but the all-pass will give it an even steeper slope. In other words, it will make the situation worse.
You want an all-pass phase characteristic that becomes more negative as the frequency approaches zero. Consider instead the following all-pass transfer function, which is just the inverse of Equation 1:
T(s) = s+w0/s-w0
Figure 6 shows the phase response corresponding to the transfer function of Equation 2. This phase function is at least in the form that you want, because it would bring down the midrange phase toward zero at lower frequencies. However, this phase characteristic is usually said to be unrealizable. The reason becomes clear if you examine the impulse response corresponding to the all-pass function of Equation 2, which is shown in Fig.7.

The impulse response of Fig.7 starts at t = 0 and extends into negative time. It is referred to as “non-causal,” because there is output from the network before there is input to it. Dennis Colin refers to this as a “crystal ball” network (2). Obviously,
a passive circuit or an op amp circuit cannot produce output before there is input. However, you can effectively accomplish this feat in the digital domain, and the method is indicated by the way the impulse response is displayed in Fig.7. If you go back far enough in time so that the impulse response has decayed as close as you require to zero, you can truncate the waveform, which you can use as a digital filter to correct the phase response.
The trick is that you first introduce an overall delay at all frequencies by shifting the impulse response in the positive
direction in time, but you end up delaying the low-frequency components less than the higher frequency ones. The price you pay is that there must be a time delay between input and output signals. This can certainly be done digitally, and it is probably not an issue when listening to music. However, it can be a problem if, for example, you are watching a movie while processing the audio with such a filter, because you may notice a time delay between the audio and video.
Crossover Solution
To verify that the filter given in Fig.7 does indeed correct the midrange phase, I loaded it into the Virtual Crossover and measured the impulse response of the midranges again, but this time the MLS signal is first processed by the filter in Fig.7 before being presented to the midrange drivers. Figure 8 shows the resulting impulse response of the midranges after applying the all-pass correction filter of Equation 2, using the filter impulse response of Fig.7. Notice the “tail” of the midrange response that occurs well before the peak. This is the result of advancing the lower frequencies in time.


The vertical line in Fig.8 shows the truncation point used in calculating the FFT in order to determine the resulting phase response, and Fig.9 shows the phase response of the midranges after the phase correction filter has been applied.
Comparison of this figure with Fig.2, the midrange phase response without correction, shows that the midrange phase response is now much flatter near the woofer crossover frequency point at 500Hz (this region is shown in white in the figure). The correction is not perfect, and it may be that a second-order all-pass transfer function might do a better job. However, I decided it was good enough for my particular application. I am using fourth-order digital low-pass and high-pass crossover filters, so the driver responses do not need to be linear very far removed from the crossover point.
Conclusion
This article shows how you can use digital signal processing techniques in a straightforward manner to accomplish the task of phase correction. There is, however, one precaution that I want to mention regarding this technique, because it can introduce some unforseen and undesirable temporal effects.
Looking again at the corrected impulse response of the midrange drivers in Fig.8, it is clear that you now have output of the midranges well before the peak of the impulse response. This is not necessarily a problem if the midrange and woofer responses are successfully combined by the crossover, because you hope the woofer response will cancel out this “precursor,” or tail of the midrange response. But I do not recommend using this technique in a frequency range that will not be crossed over with another driver.
For example, I wouldn’t recommend applying this method on the low end of the woofer in an attempt to completely flatten the woofer phase response, because I imagine that some undesirable temporal effects would be produced. aX
This article was originally published in audioXpress, January 2011.
References
1. Williams, Arthur B. and Taylor, Fred J., “Electronic Filter Design Handbook,” Second Edition, McGraw-Hill Publishing Company, 1988.
2. Colin, Dennis, “Frequency Delay Dispersion,” p. 16, aX Nov. '07.
3. Waslo, Bill, “Time, Frequency, Phase, and Delay,” Speaker Builder, p. 12, 7/96.