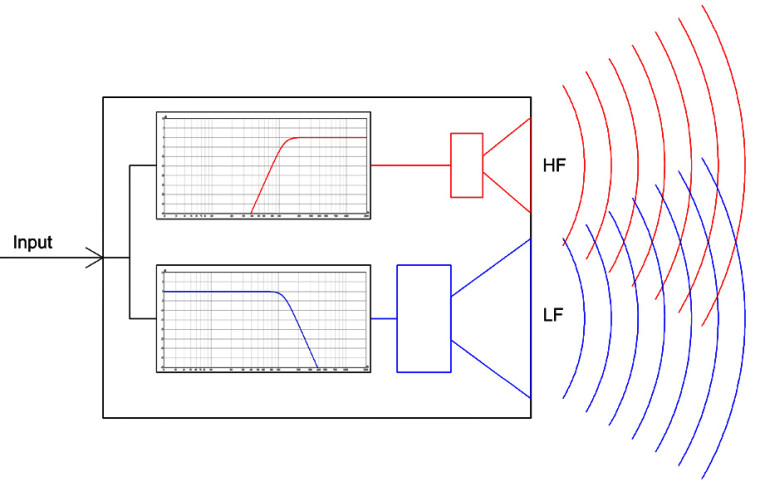
There are quite a few loudspeaker modeling programs that let users look at the on-axis frequency response of a low-frequency pass band (woofer) or a high-frequency pass band (tweeter or horn). Of course, the user has to enter the measurement data for each of the pass bands. These programs also enable the user to specify different filters that are used to alter the signals presented to each of the pass bands. The effects of the filters on each of the pass bands are calculated. The response of all the pass bands can then be added together to simulate the loudspeaker system’s on-axis response. But what’s happening off-axis?
Off-Axis
Let’s replace the on-axis frequency response data of each pass band with directivity data (on-axis and off-axis frequency responses) for each pass band (see Figure 1). We can combine this data with the effect of the filters and calculate the directivity response of the complete loudspeaker system. This might not seem like a big deal, but it can save an incredible amount of time when evaluating a crossover design. Instead of making changes to the crossover and then remeasuring the loudspeaker (which can take 30 minutes or more) in order to see the effects on the loudspeaker’s directivity, the system’s directivity response can be calculated in seconds. Keep in mind the directivity data and the filter data must be complex data (both magnitude and phase). It also needs to be sufficiently accurate for the intended purpose (see Resources).
region).
Putting It to the Test
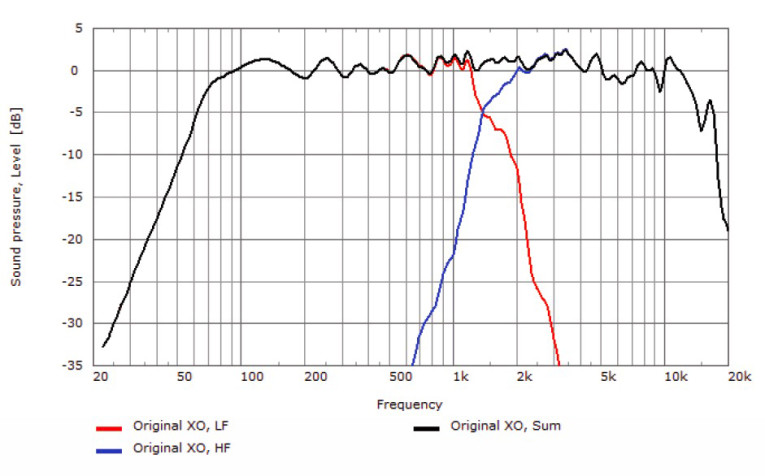
To illustrate this, we’ll use a two-way loudspeaker with a 15” woofer for the low-frequency pass band and a compression driver on a constant directivity horn for the high-frequency pass band. The horn is located above the woofer, vertically. This can often make for a less than ideal vertical directivity response. The on-axis frequency response of the low-frequency and high-frequency pass bands, along with the combined summation, using the original crossover filters from the manufacturer of this loudspeaker system are shown in Figure 2. This seems to show good summation through the crossover region (from about 1 kHz to 2 kHz).
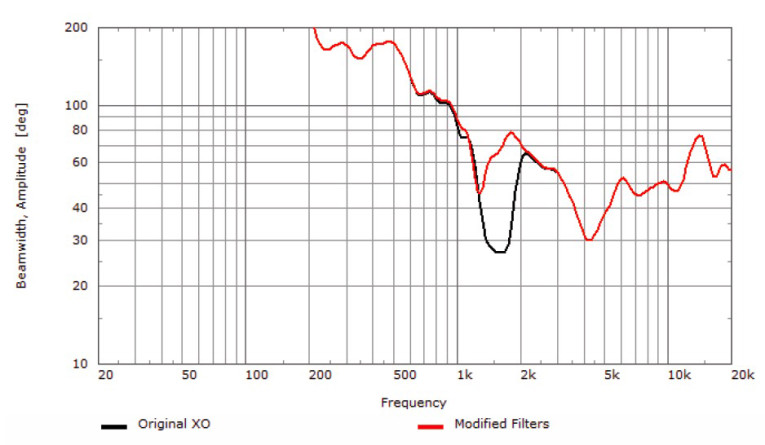
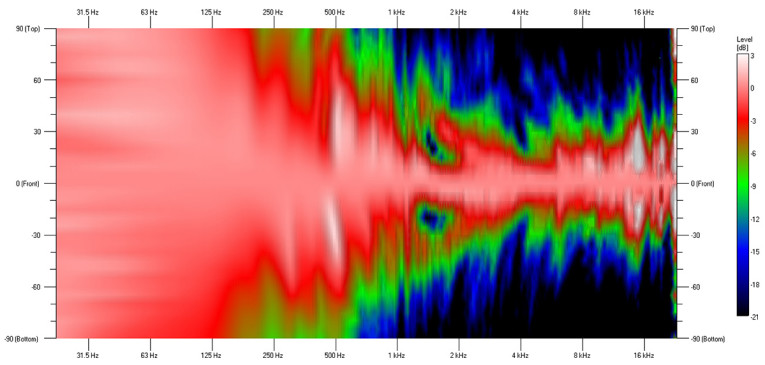
However, when we look at the vertical beamwidth (see the black curve shown in Figure 3) and the vertical directivity map (see Figure 4), we see that there is a problem in the crossover region. The beamwidth, or coverage, of the loudspeaker narrows considerably from a desired value of about 60° to less than 30° in the 1 kHz to 2 kHz crossover region.
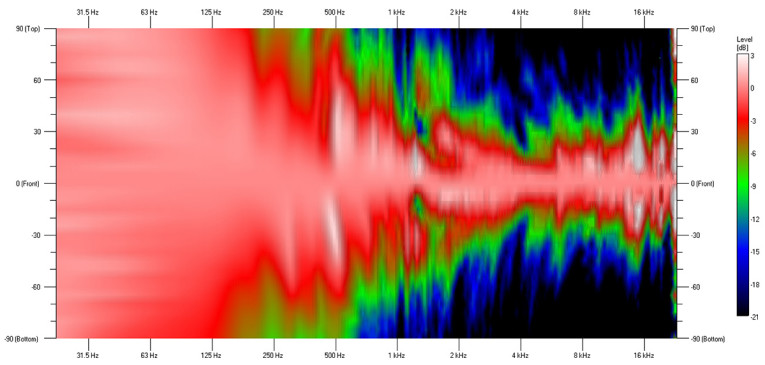
By applying a few different parametric equalization filters to the low-frequency and high-frequency pass bands, the vertical directivity can be improved (see the red curve shown in Figure 3 and the vertical directivity map shown in Figure 5). This improvement might have taken days to realize if new measurements of the vertical polar response had been required after each tweak of the new equalization filters. By using the loudspeaker modeling data files for the individual low-frequency and high-frequency pass bands, the changes and optimization of the system directivity was accomplished in a few hours.
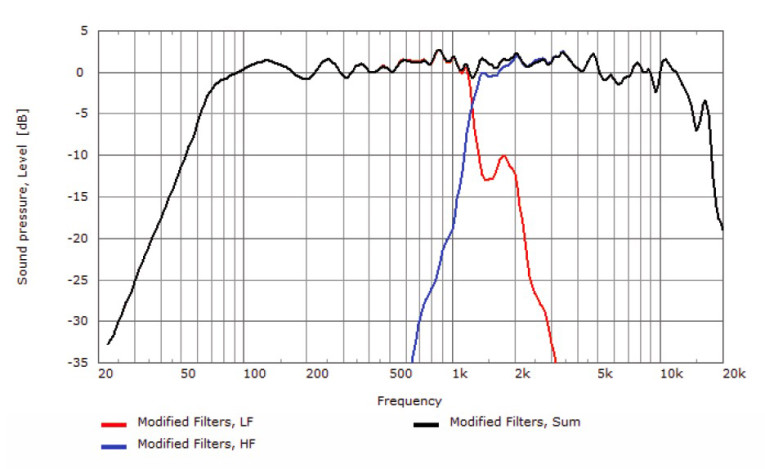
The on-axis frequency response of the low-frequency and high-frequency pass bands, along with the combined summation, using the modified filters are shown in Figure 6. Compared to Figure 2, the summation through the crossover region is good, however, the level of the low-frequency and high-frequency pass bands is higher to get the same overall SPL though the crossover region. This is due to the change in the relative phase response between the low-frequency and high-frequency pass bands, which is required to achieve the more uniform vertical off-axis response.
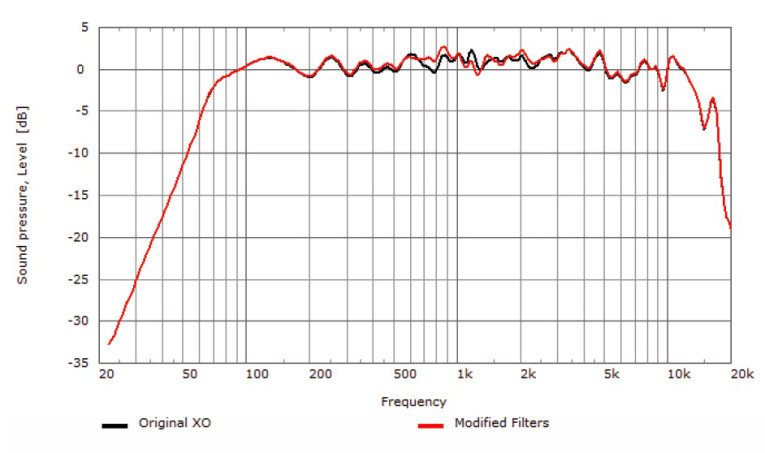
A comparison of the on-axis responses using the original crossover and the modified filters shows that there has been almost no change to the on-axis response (see Figure 7). A comparison of the vertical directivity maps (see Figure 4 and Figure 5) shows the off-axis response is now much more consistent, as well as being more similar to the on-axis response.
Modeling Programs
The program I use most for modeling the directivity of loudspeaker systems and for crossover design is SpeakerLab (from AFMG). A nice feature of SpeakerLab is that it calculates the broad band level of the signal driving the individual pass bands. If the maximum input voltage (MIV) has been entered in the data files for these pass bands, then SpeakerLab is able to determine the maximum input level for the complete system. The maximum level for the loudspeaker system is based on the spectral content of the input signal to the loudspeaker system, as well as the crossover and EQ filters used for each of the pass bands. This feature can help provide a good indication of the maximum continuous SPL that the loudspeaker system can produce.
Using our two-way loudspeaker example, the MIV level for the high-frequency pass band is 23 dBV. This is an RMS voltage of about 14.1 V, equivalent to approximately 25 W at 8 Ω (the rated impedance of the high-frequency driver). Note that MIV is not the same as “power handling” for a loudspeaker. The MIV level for the low-frequency pass band is 31 dBV, an RMS voltage of about 35.5 V, which is equivalent to approximately 300 W into 4 Ω (the rated impedance of the low-frequency driver).
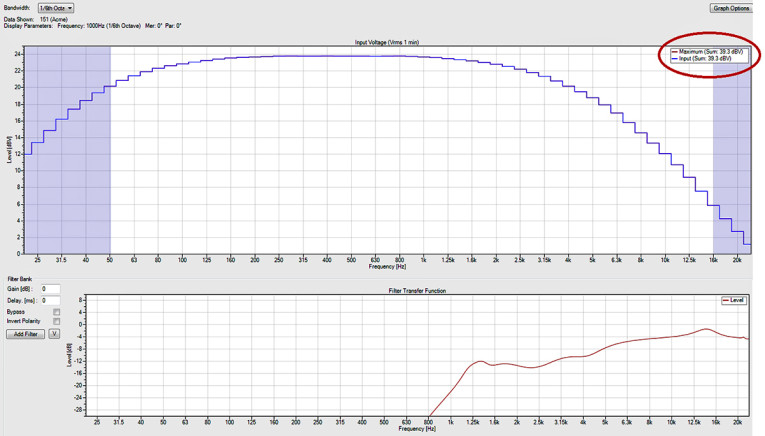
Let’s look at some screenshots from SpeakerLab (see Figure 8 and Figure 9). From these we can see what the maximum input level to the system (upstream of the filters) is when the effects of the crossover and EQ filters are taken into account. The maximum input level to the system based only on the high-frequency pass band and its filters is 39.3 dBV (92.3 V). We have basically muted (disconnected) the low-frequency pass band from the system to determine what the high-frequency pass band can do all by itself.
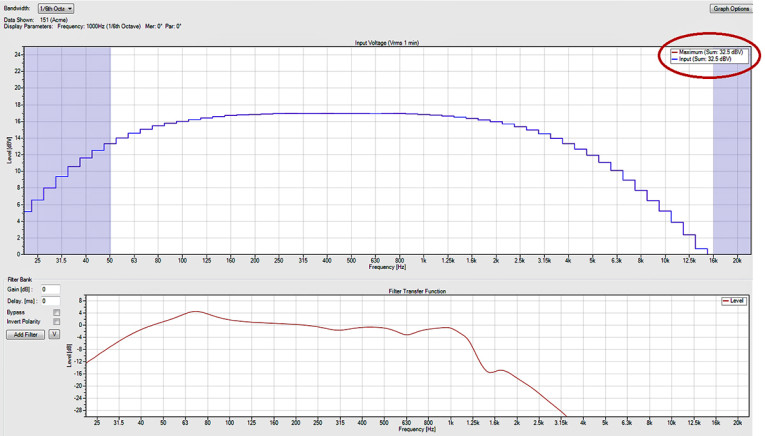
We can then reverse this and mute the high-frequency pass band so that only the low-frequency pass band is being used. The maximum input level to the system based only on the low-frequency pass band and its filters is 32.5 dBV (42.2 V). This is about 7 dB lower than the maximum system input level based on the high-frequency pass band. The low-frequency pass band will be the limiting factor for the maximum input for the system, which will be 32.5 dBV.
The Results
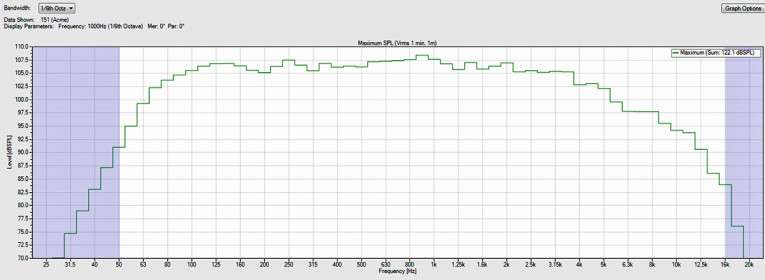
This analysis is based on an input signal having the spectral content specified for the IEC 60268 noise test signal. There is a rolloff of the low frequency and high frequency energy in this signal (see the blue curves shown in Figure 8 and Figure 9). It approximates the spectral content for an average of many different types of music and speech. The results of our analysis might be different for other input signals with different spectral content (e.g., pink noise). With the IEC 60268 signal at an input level of 32.5 dBV to the loudspeaker system, the maximum continuous SPL that it should be able produce is about 122 dB, referenced to 1 m (see Figure 10).
Hopefully this has provided some insight into a few of the benefits of using full directivity loudspeaker modeling data for each individual pass band. Next time, we’ll look at what kind of testing is required to determine the MIV for the individual pass bands of a loudspeaker system. For additional information on modeling the directivity of loudspeaker systems read “Simulating the Directivity Behavior of Loudspeakers with Crossover Filters,” an Audio Engineering Society (AES) paper written by Stefan Feistel, Wolfgang Ahnert, Charles Hughes, and Bruce C. Olson. VC
Resources
S. Feistel, W. Ahnert, C. Hughes, and B. Olson, “Simulating the Directivity Behavior of Loudspeakers with Crossover Filters,” 123rd Audio Engineering Society (AES) Convention preprint #7254, October 2007.
C. Hughes, “Measurements for Loudspeaker Modeling Files,” Voice Coil, April 2017.
Source
SpeakerLab
AFMG Technologies GmbH | www.ease.afmg.eu
This article was originally published in Voice Coil, August 2017.