Three audio experts discuss the role of distortion levels in what we hear. The debate was caused by an article titled “Amplifier Musicality - A Study of Amplifier Harmonic Distortion Spectrum Analysis” by Jean Hiraga, which originated comments by Jan Didden, Dennis Colin and a subsequent response by Jean Hiraga. The original article appeared in audioXpress March 2004 and the resulting conversation was published in audioXpress October 2005.We start by transcribing the first part of Jean Hiraga’s article.
Modern amplifier designs are nowadays capable of very low measured harmonic distortion, on the order of 0.005% or even 0.0005%; levels which can only be measured with elaborate test instruments. Despite this state of affairs it is interesting that valve amplifiers, which often have a distortion level at least 100 times greater (e.g., 0.5%) may sound subjectively no more, and can sound a lot less, distorted than transistor designs in spite of the higher measured level. This causes endless debates between the “golden eared” listener and the engineer one quoting the position of the distortion meter needle; the other talking about the special tone of piano x of year y.
This article does not intend to discuss in detail the relationship between a particular electronic circuit design and its subjective result, as this is far too large an undertaking. However, some particular measurements have been made which may help to reconcile the engineers and the listeners. This is not simply a question of taking certain measurements or conducting blind listening tests on amplifiers, but an attempt to show that a particular measurement may result in an indication of the ability of an amplifier to reproduce a musical sound.
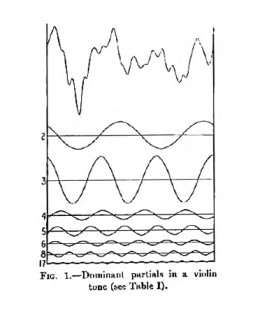
Figure 1 and Table 1 (See Figura A1,2,3) show the spectral composition of a violin note with its various harmonics and their relative levels. It is important to note that the tonal color or “personality” of the violin lies in the high-order harmonics from the 4th to the 20th, whose levels are extremely low compared with the second or the third. The slightest modification of the relative levels of these harmonics will change the spectrum of the signal fed to the loudspeakers and hence the tonal “color” of the violin, making a Stradivarius sound like a very cheap violin, for example.
This spectrum analysis technique can also be applied to audio amplifiers, but as yet few people have been interested enough to analyze the actual content of the measured distortion (whether 0.5% or 0.0005%). However, the particular pattern of harmonic distortion in an amplifier is extremely significant and can provide important indications of its subjective qualities; it is not necessarily wrong to refer to “musicality of distortion.”
Response by Jan Didden
It is with hesitation and timidity that I should cross (s)words with such an eminent audio personality as Jean Hiraga, but this hesitation and timidity is overridden by my search for technical correctness and understanding.
In his article (“Amplifier Musicality,” aX March 2004, p. 32), Mr. Hiraga discusses the distortion spectra of various amplifiers. According to his experience, there is a correspondence between a gradual decrease of higher harmonic components and the subjective quality of an amplifier. In particular, amplifiers where the harmonic distortion spectrum does not monotonically decrease, or where specific harmonics are absent, may sound less agreeable even if the absolute distortion levels are very low.
Mr. Hiraga argues that higher distortion levels are not in themselves objectionable if the harmonic components show an orderly, monotonous decrease. Reference is made to a violin, which produces a sound that also shows many (up to 20) harmonic components. Any change in the relative amplitude of these components would alter the “color” of the violin.
One transistor amplifier, #2 (Fig. B), shows an almost total absence of harmonic components beyond the third. At the end of the article Hiraga discusses amplifier #11 (Fig. L), a single-stage WE300B, which shows a near-perfect row of gradually decreasing harmonics.
Mr. Hiraga then continues, and this is where I part with him: Amplifier #11 would reproduce all the harmonics of a violin very well, while amplifier #2 would truncate the violin spectrum, absorbing it in the feedback. I am surprised by this statement, which is clearly and fundamentally wrong.
Assume for the sake of discussion that a hypothetical violin would produce a 1kHz sound plus two harmonics, each 20dB lower in amplitude than the previous one (the 2nd harmonic being 20dB below the fundamental). It is understood that the actual violin spectrum is much more rich, but just these few harmonics in the analysis will prove the point. Also assume that amplifier #2 has only a 3rd harmonic distortion component at 80dB below the fundamental (Fig. B). This amplifier #2, in reproducing the violin sound, would add a 3rd harmonic to all source components at −80dB below the original level.
It becomes more complex with amplifier #11 (Fig. L), which would add many harmonic components to each original violin component, with each additional component some 10dB lower than the previous one, and the first harmonic (the 2nd) 20dB below the fundamental. To keep this manageable, I have looked at only the first three harmonics (2nd, 3rd, 4th) produced by amplifier #11. I have tried to capture the resulting spectrum in each case in Table 1.
One point is immediately clear: It is amplifier #11, with the rich, monotonous decreasing distortion spectrum, that alters the spectral composition of the hypothetical violin much, much more than amplifier #2, which shows predominantly 3rd harmonic distortion. Why, then, would listeners prefer (if this is indeed the case) this strongly altered spectrum to the original one?
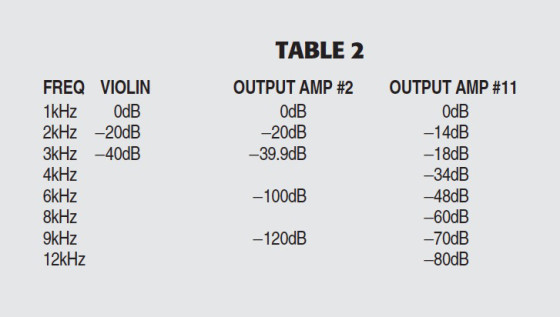
One theory could be that although amplifier #11 alters the spectrum much more, it better preserves the spectral shape than amplifier #2. Table 2 shows that this also is a false assumption: Amplifier #2, with its seemingly ugly 3rd harmonic spike, has only a very, very benign impact on the violin spectrum. Amplifier #11, however, is terrible. Not only does it significantly alter the spectrum content (it adds 4, 6, 8, 9, and 12kHz components, which are totally absent in the original), it also significantly alters the spectrum shape.
The 3rd harmonic at the output of amp #11 is more than ten times as strong as in the original of amp #2. The ugly 9th harmonic is fully 50dB stronger at amp #11 than at amp #2. It seems to me that the conclusion is inescapable. Amplifier #11, for all of its nicely, monotonously decreasing harmonic spectrum, totally messes up the violin. If listeners nevertheless prefer a type #11 amplifier, it is not because it more faithfully preserves the original spectrum, because it doesn’t. It must be because listeners prefer a heavily mutilated spectrum to the original source.
Response by Dennis Colin
Regarding “Amplifier Musicality,” by Jean Hiraga, I’ll start with the article’s fundamental premise: “Even though the distortion in an amplifier may be at extremely low levels, the content …must conform to the laws of harmonic levels in order to give subjectively musical reproduction.” (These “laws” are referenced to Olson’s observation that pure tones don’t sound musical, but a regularly reduced harmonic structure can.)
That an amp’s distortion, if well below audible threshold, must conform to “musicality” should be obviously questionable. Consider “Single-Ended vs. Push-Pull” by Scott Frankland (Stereophile, Jan. 1997): He notes a resemblance between the distortion spectra of a certain amplifier and the ear, and then comments that this “…does not in any way justify the presence of distortion in playback systems.”
Mr. Hiraga shows a sample violin note spectrum, then says, “The slightest modification of the relative levels will change …the tonal color …making a Stradivarius sound like a very cheap violin…” Really? Moving one’s head an inch (let alone bowing the violin differently, and so on) will more than slightly change the spectrum! But a Strad still sounds like a Strad, because something in the harmonic patterns - how they dynamically change - and in harmonic sounds is identifiable.
Finally, Mr. Hiraga says about amplifier 11: “A violin, in particular, is reproduced very well as harmonics 2 to 20 pass without interference in their relative levels…” Unfortunately, with about 9% THD (Fig. L, p. 35), a pure organ stop will also be reproduced with violin-like harmonics!
Some of the amplifiers have all harmonics below 70dB. At moderate SPL the ear can generate 1% THD (−40dB). So it seems ludicrous to attribute anything to the structure of such an amp’s distortion. Of course, static single-tone distortion bears about as much relation to that produced by an amp delivering music to a reactive load as kicking tires does to driving the car!
If the spectra shown maintain their shape but the levels increase greatly in the real world of complex music waveforms and reactive speakers (a big “if”), then the added harmonics may blend in with, or fill in recorded losses of, natural instrument harmonics. But even if this is possible, to generalize a correlation of the figures shown to overall “musical performance” is absurd.
Jean Hiraga respondsHigh fidelity is the closest possible reproduction of the original. With regard to an amplifier, this means that the output waveform must in all respects respects be the amplified exact replica of the input signal. Subjective high fidelity is a different matter because it must take into account personal appreciation of a listener. This aim is attained when the listener declares to have the same aural sensation that he would have had in a concert hall or in a studio.
The ear remains the judge of fidelity, faced with the various types of distortion such as frequency distortion, phase distortion, transient distortion, IM and IIM distortion, scale distortion (intensity distortion), frequency modulation distortion, amplitude distortion, and harmonic distortion.
If measured harmonic distortion can take into account individual levels, aural sensation of harmonic distortion must refer to fundamental aspects of tone quality that are sonance (the successive presence of fusion of timbre continuously changing, the pitch, and the sound intensity in a tone as a whole) and the timbre (defined by the simultaneous presence of fusion of the fundamental frequency and its partials at a given moment).
Since 1924, R.L. Wegel and C.E. Lane have found effects of auditory masking of pure sound by harmonics or by other tones (1). It is well known that harmonics added to a pure tone are not necessarily displeasing, since voices, sounds of various origins, and music instruments produce notes made of a complex family of harmonics. Wegel and Lane were also among the first to discover that harmonics of defined intrinsic levels added to a pure tone can be heard as a pure tone by successive mask effects and multiple harmony incidence.
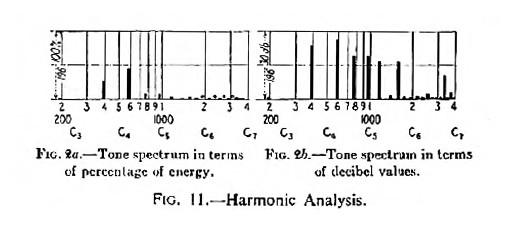
Concerning the same matter, it is important to take into account the fundamental work of Carl E. Seashore (2) in his book “Psychology of Music”. In my article, Fig. 1 shows a sample of violin and its relative levels. The original article, published 25 years ago in Nouvelle Revue du Son, mentioned that that figure was from Psychology of Music.
In his book titled “Loudspeakers, The How and Why of Good Reproduction”, G.A. Briggs of Wharfedale Wireless Works refers to the same work of Seashore as follows “Harmonic analysis: At this point, it may be of interest to see what actually constitutes a musical tone heard by the ear. This is found out by harmonic analysis. An example from Seashore’s Psychology of Music gives the tone spectrum of a open G string of a violin played with medium intensity. It will be noticed that there is only 0.1% of energy of the fundamental frequency of G 196, and this shows why the fundamental can be omitted from reproduction without destroying the pitch of the note. This fundamental is established by the difference-tone of 196 which occurs between the overtones. The top wave of the figure is an oscillogram of the full tone, which was analyzed up to 20 partials, covering a total frequency range of about four octaves. When one reflects that a single note has such a complicated structure, it is difficult to imagine the thousands of wave formations produced
by a full orchestra…” (Fig. A1,2 3).
Seashore takes into account the same matter in another of his works, “In Search of Beauty in Music.” In “The perception of Music, psychological origins and development of the sense of Tonality,” authors Robert Frances and W. Jay Dowing developed a similar point of view.
It is important to keep in mind that Wegel, Lane, and Seashore didn’t have at their disposal enough pure sound generators to develop their investigations more completely. In the ’40s, a lot of works by authors such as H.A. Hartley (3), IEE Radio Section (4), and, more particularly, H.F. Olson (5) in “Elements of Acoustical Acoustical Engineering,” related the importance of harmonic distortion spectra classed in categories such as “perceptible, tolerable, and objectionable distortion.” In his single-stage 2A3 triode amplifier, Olson stated that he obtained distortion levels of −30dB, −50dB, and −70dB for 2nd, 3rd, and 4th harmonics. The last −70dB, or 0.03% corresponding to the audio generator self-distortion, explains why Olson was unable to measure respective levels of 5th and higher order harmonics.
Also, keep in mind that in amplifiers, classical push-pull operation leaves the third and odd harmonics predominant. In tube circuits, if the grid modulation level is increased to give the same value of total distortion as on the single triode circuit, the high order harmonics become more significant and unmasked by first harmonics. If this remark applies to sounds of relatively slow attack and decay, this effect is largely overshadowed by the more prominent influence of transient sounds, including a large part of inharmonic content added to the harmonic content, as explained in an article of A.W. Ladner (6) titled “The analysis and synthesis of musical sounds.”
A unique faculty of the ear is to establish timbre personality and fundamental notes by successive analysis of harmonics starting with the highest order ones, as stated in various works of S.S. Stevens, Von Bekesy, and E. Zwicker. This is why our brain has the ability to reconstitute a fundamental note from listening to its partials (this was tested by Carl E. Seashore). If the amplifier induces partial or total suppression of some harmonics among those forming THD, this is taken in account by the ear which will detect a corresponding timbre.
This does not exclude the masking effects, more particularly, those for which harmonics relations and relative levels conduct to hear a unique pure tone, referring to extensive works conducted by H. Sakai (7) in his “Harmony and distortion” paper published in 1980 or by a Japanese group titled The Fukuoka Distortion Society.
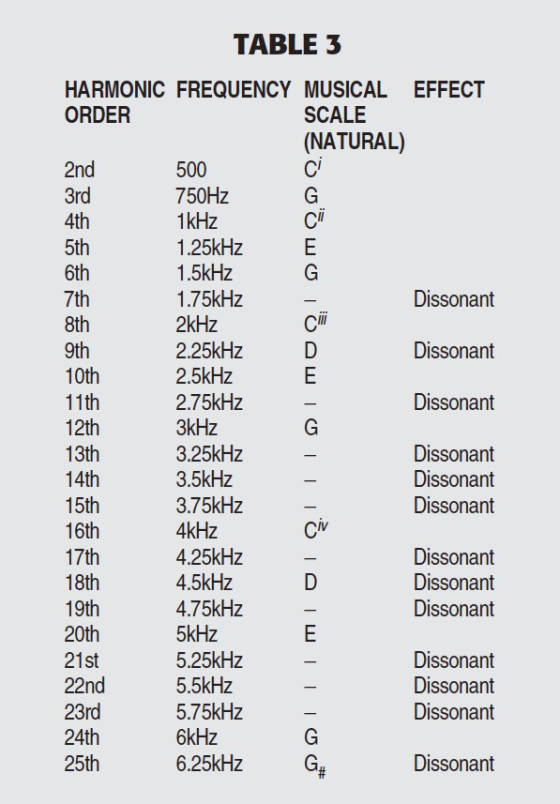
It is, however, important to say this “works” only for THD values under about 3%, confirming the experiments conducted by H.F. Olson with 2A3 single-stage triodes. The study of acoustics, psychology of music, and violin sounds may be interesting ways to understand the subjective effect of some harmonics in relation to naturalness and beauty of sound. But for easier understanding, refer to Table 3, which shows a fundamental frequency of 250Hz and its harmonics from 2nd to 25th, as well as related dissonant effects.
In the field of violin study, works of world authorities such as Carleen Maley Hutchins (7) and Fernand Dacos (during his work at Conservatoire of Liege, Belgium, in the 50s and 60s, he had the opportunity to analyze more than 1,500 violins) detailed with accurate measurements harmonic relations and respective levels, including the effect of the shape of audibility curves to the ear and its maximum sensitivity of around 3kHz. Their conclusions are similar to those found by A.W. Ladner. A third octave analyzer can show that most sound energy produced by musical instruments is concentrated between 50Hz and about 1.5kHz.
Harmonics are spread out to the upper limits of audibility, with respective levels decreasing very fast above 5kHz, in areas where “bad musicality” amplifiers produce irregular high-order harmonic distortion unmasked by first-order ones.
Concerning harmonic distortion spectra shown in my article, I must add the following:
• In amplifiers, regular decay of harmonic distortion spectra is not always proof that the circuit doesn’t selectively absorb some harmonics, especially in the case of unconventional complicated circuits.
• Slight asymmetric switching distortion induced by a push-pull circuit or by poor quality output transformers may generate a series of harmonics that can be the cause of confusion between good- and bad-sounding amplifiers.
• A harmonic distortion spectrum with a regular decrease may change with fundamental frequency and level and modify sound quality accordingly.
• In a classic amplifier made of several stages, each stage has its proper characteristics input/output transfer curve, linearity, harmonic distortion and is affected by other kinds of distortion in static (constant level, fixed frequency) or in dynamic/transient mode. In dynamic and transient mode corresponding to normal music and sound conditions, these phenomena and nonlinearities are not simply added or subtracted from others. They are the cause of very complex transient cumulative effects of nonlinearities that change with each tiny portion of amplified and reproduced signal on real (complex) loads.
Dennis Colin raises an important point concerning an amplifier’s delivery of sound to a reactive or to a real load and effective back energy (CEMF energy) released by the loudspeaker. An article of mine published in Revue du Son & du Home Cinema (8), concerns an experiment that was conducted 20 years ago by a group from Tokyo Musashino University in Japan. The experiment simulated back energy of a loudspeaker comparing its effects on a pure or a real complex load, while the amplifier under test was stimulated by another frequency.
The published results limited (because of lack of space) to four amplifiers revealed very interesting dynamic comportments of each amplifier in that condition. In that article, Fig. 1 shows original signal spectra with pre-filtered 50Hz applied directly to the load and the 1kHz signal applied
to the input of the amplifier; Fig. 2 illustrates a good example of an amplifier not influenced by this condition; Figs. 3 and 4 show two other examples of amplifiers exceptionally good under normal measurement conditions, each using different complex active feedback, showing on that test important generation of harmonics that would be a good explanation concerning their “inexplicably harsh and brittle-sounding” output; and Fig. 5 shows a single-stage amplifier (801A), with formation of harmonics and subharmonics with “paradoxically” a quite tolerable subjective distortion effect due certainly to regular decay envelopes.
A lot of matters that cannot be easily explained still remain, especially because we are still unable to access ultra-fast measurements in real working conditions, underneath the musical signal. It is now an established fact that significant subjective differences of sound quality can be noted between several kinds of resistors, capacitors, and coils (of loudspeaker networks), even if their harmonic distortion spectra are extremely low (–100dB or below), or 20 to 30dB below floor at audition.
Concerning this point, note that the form of harmonic distortion induced by such components is frequently similar or very close to the same form of harmonic distortion “lifted” in audible levels. A good example is the case of some high-priced ultra-high stability resistors using the method of tiny matched positive and negative thermal elements that sound worse than a version using, for example, a pure tantalum oxide single resistive element.
I prefer not to enter into the domain of “sound of cables” or into the matter of “sound of passive components,” because I know the influence of my first articles published on this matter in Nouvelle Revue du Son and in L’audiophile review from 1976 and 1977. Conventional measurements, made with even very sophisticated and ultra low distortion meters, are still producing mostly insignificant results, because they are located largely under the floor of audibility. AX
References
1. R.L. Wegel and C.E. Lane, “The Auditory Masking of Pure Tones,” Physical Review, 23, 266-285, 1924.
2. Carl E. Seashore, “Psychology of Music,” Mc-Graw-Hill, New York.
3. H.A. Hartley, “Aesthetics of Sound Reproduction - High Fidelity or Judicious Distortion?” WW, July/August 1944.
4. “IEE Radio Section, DistortionDoes it matter?,” WW, January 1949.
5. H.F. Olson, “Elements of Acoustical Engineering,” Van Nostrand, 1947.
6. A.W. Ladner, “The Analysis and Synthesis of Musical Sounds,” Electronic Engineering, October 1949.
7. H. Sakai, “Harmony and Distortion”, N.H.K Journal, 1980.
8. J. Hiraga, “La Distortion dans tous ses états,” Revue du Son & du Home Cinema, n°279, November 2003.
