The question is: Is it possible to transform a conventional expansion horn (exponential, hyperbolic sine, hyperbolic cosine, catenoidal, tractrix, spherical, etc.) into a constant directivity horn?
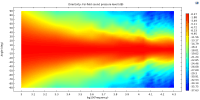
We need to consider a mathematical expansion law of a horn not only as an expansion in terms of an area, but also in terms of a volume. If we keep the defined horn expansion law following the same volume expansion, within certain limits, we can modify boundary profiles to satisfy special needs. The need we want to satisfy is the constant directivity. As we know, the directivity of a horn is controlled down to a frequency that has a wavelength comparable to the horn mouth.
Horn.ell.a is a software designed in 2006 and its algorithm doesn’t follow Cartesian profiles, as per the usual approach with a horn, but it works on volumes. With the volume process, it is possible to extend expansion profiles for a progressive match between the throat and the different mouth shapes.
The horn’s mathematical progression is always guaranteed, so the key is to have a non-deformable volume gradient. In this way, if we want a hyperbolic exponential profile, we will maintain the same load and low-frequency control, but we can also obtain the directivity control on one plane.
Read the complete article available here.
This article was originally published in Voice Coil, December 2019.