
The fundamentals are easy, or rather, they are once you look at them from the proper perspective. Like most people who pay attention to phono cartridge alignment in a pivoted arm, I watch the needle traverse the black disc in search of understanding. At the lead-in and outer reaches, the tracking error was obviously “wide” of the spindle — that is, a perpendicular from the stylus passed outside of the turntable’s spindle. As play continued, the LP pulled the cartridge into, and then past, alignment, until the tracking error was “inside” the spindle. This is where it stayed for the bulk of playback until, close to the end of the side, the LP pulled the needle back into alignment and, finally, for the last couple minutes of playback, past perpendicular to the “wide” side again.
Finding The Angle
I knew these to be the inevitable consequences of a pivoted arm with a cartridge set to overhang the spindle and then offset at an angle to minimize the tracking error. This gives two points in the arm’s arc where the stylus is at 90° to the groove (the “nulls”) with varying degrees of error elsewhere. It is an exercise in compromise. I knew this, but full realization didn’t occur until I saw Keith Howard’s article in Stereophile (March ’10) and took an interest in an illustration. I then saw that if you consider the stylus fixed and let the turntable move as playback proceeds, understanding the geometry involved becomes obvious, trivial.
The second part of this piece walks you through an example, but the basics are these: The distance from pivot to spindle stays the same, and is known, as is the distance between the chosen nulls. So you have an isosceles triangle whose base is the null-to-null dimension and whose sides are the pivot-spindle dimension. Thanks to Pythagoras, you can find the length of a line from the midpoint of the base to the apex (arm pivot point).
In addition, because you know how far away from the spindle you want the inner null, the second leg of a right triangle is known. Again, thanks to Pythagoras, you can calculate the hypotenuse, which is arm length. With all three dimensions of a right triangle in hand, you can consult some trig tables (I used tangent) and find the offset angle. That’s it.

Catnip For DIYers
The possibilities are manifold. You can adopt the sort-of conventional nulls at 66 and 121 mm and sort out the pivot spindle dimension, given arm length. Or the other way ‘round. Or, given a pivot-spindle number, you can figure arm length for whatever nulls you like.
You can give preference to low error in the close-in real estate (i.e., radius inside 60 mm or so) or not. Set up a turntable for the peculiarities of 7″ 45s or 10″ 78s. Or take measures to accommodate those true oddities, 16″ (pre-tape) transcription discs. Or build yourself a 15″ balsa monster. Go nuts, or at the very least, scribe your own alignment setup disc from a scrap LP. See below.
A Word About Tolerances
One of the charming features about the alignment setup table I used to use was that it gave dimensions and offset angle to about six places. You will be relieved to note that I’ve limited myself to final tolerances of about 0.1 mm and a tenth of a degree or so. I figure this is the order of resolution that can be sensibly expected in the field. Beyond that, factors such as off-center LPs, the vagaries of cartridge manufacture, and stray (bias and warp-related) cantilever deflection make a mockery of six-digit tolerances. Use a good ruler and straightedge if you scribe your own disc, and a lot of light and cheap reading glasses during the setup, and you’ll be fine.
A Cartridge Need
Keith Howard makes the excellent point in his article that the needle-mongers haven’t exactly covered themselves in glory when it comes to easing the setup chore. He plumps for boxy bodies at a minimum, but prefers a shoe attachment with extended parallel sides and stylus location clearly indicated.
Not good enough, I say. Needles with user-replaceable stylus inserts should also be provided with alignment-friendly inserts that fit into the body like the stylus assembly does. A pointer, beginning at the stylus’ position and extending at 90° toward the table spindle and long enough (say, 100 mm) to be useful would do the trick. Moving coil units should be supplied with a removable stylus guard that serves the same purpose. Or, a groove might be machined into the top of the body, suitable to accept a pointer—a thin wire, perhaps—to accomplish the offset adjustment.
This is an area where the manufacturers, with a little care and forethought, at virtually no cost, could provide a feature that will genuinely endear them to their customers.
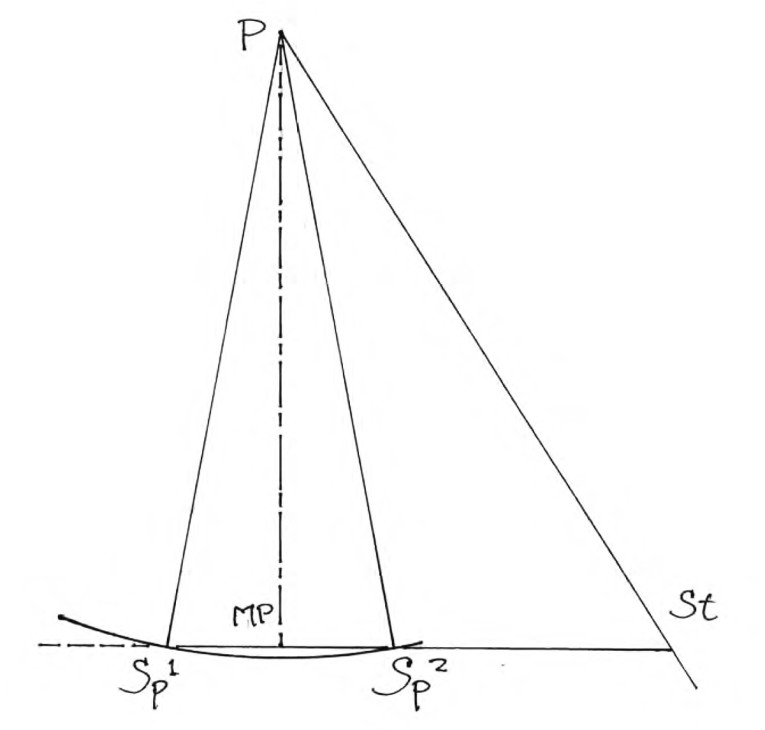
A Setup Example
Figure 1 represents a setup for a turntable with a pivot-spindle distance of 150 mm and nulls at radii of 66 and 120 mm. P is the arm pivot; SP1 and SP2 are points on the arc selected as nulls as the turntable moves from leadin groove (at the left, r = 145 mm) to the end of modulated territory at the right (at r = 60 mm). Sp is short for spindle. St is the point at which the stylus resides, held stationary here for simplicity’s sake. Because nulls are at r = 66 and 120 mm, you know they’re 54 mm apart, which distance forms the base of an acute isosceles triangle with sides of 150 mm each (the P-Sp dimension).
The midpoint of the base (MP) is 27 mm, so putting Pythagoras’ theorem to work, you find the line from MP to P is about 147.55 mm long. I set the inner null (SP3) at 66 mm, so you know MP-St is a total of 93 mm. Resorting again to Pythagoras, you find that P-St, which is the arm length, comes to 174.41 mm. (Overhang, which isn’t really relevant to these proceedings, comes to 24.41 mm.) You now have both arm length and pivot to spindle dimension. All that’s left is offset angle.
For this number I resort to some basic trig tables. You can find the angle defined by MP-St-P by calculating its tangent (147.55 mm divided by 93 mm), which is about 1.5865, which corresponds to an angle of 57° 46°or about 57.75°. Subtract that from 90° and you have your offset angle: 32.25°.
Using a 150 mm pivot-spindle dimension makes for an admittedly lousy turntable, but a pretty good example. Sensible arms and layouts result in very skinny isosceles (P-SP1-SP2) triangles. This example exaggerates some important features.
The figure provides a good intuitive notion of alignment change as the turntable moves from lead-in at the far left through the nulls to the inner radius, set at 60 mm here. Before the first null (SP1) the spindle is above the line and the offset angle is insufficient. Between nulls, the spindle is below the line and the offset angle is too great. Beyond the second null, the spindle is again above the line and the offset angle errs to insufficiency. This is the source of the swoopy graphic you see depicting tracking error.
From Qualitative To Quantitative
Are you curious to tag an actual number to tracking error? You can do that. The easiest is error at the bottom of the arc, below MP. We know P-SP is 150 mm and P-MP is about 147.55 mm, so the arc is about 2.45 mm below the line at MP. Error will be the angle whose tangent is (2.45 mm divided by 93 mm) 0.02634, or nearly 1.5°. If you remember a little high school geometry and algebra, you can cipher out the error at the maximum for the arc below the line (very nearly, but not the same as the error at MP figured above) and at the maxima at lead-in (r = 145 mm) and lead-out (r = 60 mm, maybe). I won’t go through it here, but it involves right triangles with a common side and, as I warned above, a little simple algebra.
For most people, just sketching out a scale diagram will give enough of a conceptual handle on the problem to satisfy. Remember that distortion derives not from tracking error alone, but from error weighted (i.e., divided by) distance from the center of the LP. So be more ruthless about your inner null point and minimizing the “belly” below the line between nulls. Nobody would argue too strongly against nulls at 64 and 118 mm. Or go to a longer arm.
Rolling Your Own Setup Disc
This is a cheap, easy, and only minor chore which will amaze your friends. Look again at Fig. 1 and observe that once you’ve settled on your nulls, it matters not at all what your pivot-spindle dimension or arm length is — this setup disc will work. This approach rests on the midpoint-pivot line; all changing the pivot-spindle dimension does is change the sides of the isosceles triangle. Using the same nulls as in the example above, here’s how to produce your own alignment disc:
1. Take a scrap, flat LP. Spray-paint it white. Let dry.
2. Using a sharp needle or similar scribe and a good straightedge, cut a clean line through the paint from the LP edge through the exact center of the hole, and about 2″ beyond. This is your radius (r).
3. With an accurate ruler, make small marks on r, first at 27 mm either side of the LP center, then at 66 mm and 120 mm. The tics at 27 mm on either side of the center correspond to MP for the two nulls. The tics at 66 and 120 mm are the two nulls.
4. Take a good right angle and scribe two long parallel lines, from bead to bead, one through each of the tics at 27 mm either side of center and perpendicular to r. Then scribe a shorter perpendicular, long enough for convenient offset angle alignment, through each null point on r, at 66 and 120 mm in this example. Other than any notes you may want to add to the disc, you’re done.
Using the disc is a two step process. Step one is alignment at outer (120 mm) null. Put the disc on the table with r extending to your right. Sighting down the long line to the right of the spindle, adjust the disc until this line points precisely at the arm’s pivot, then tape things down so they don’t shift. Now fiddle with the arm and cartridge so the stylus rests exactly on the 12 0mm null point on r and is parallel to the 90° line scribed through r. This corresponds to the spindle at SP1 and stylus at St in Fig. 1.
Step two is checking alignment by confirming alignment at the inner null. Lift the arm and shift the disc slightly so the long line to the left of the spindle points precisely at the arm’s pivot, and locks things down again. Now swing the arm over; the stylus will not only rest on r at exactly the inner null point, but it should be in alignment here, too… assuming you got things right in step one.
This corresponds to spindle at SP2, stylus at St in Fig. 1. (Note: You can use this particular disc for any setup with nulls 54 mm apart. Just mark your different nulls on r and have at it. I should also note that this approach to alignment isn’t original to me. A friend has a disc — just one sighting rail instead of two — made years ago by, oh, I can’t remember… Geodisc? I do remember wondering about the thinking behind the methodology. Now I know, and so do you.)
Contributors
Tom Yeago (“Cartridge Alignment for DIYers”), who obviously has too much free time, has been a buff since puberty, or thereabouts. A Virginian (the Shenandoah Valley), Tom’s formal training is in economics, a.k.a the dismal science. Besides noodling about in hi–fi matters, he also devised a complete reorganization scheme to fix the shamefully inadequate public school system, in case you’re interested.
John Sunier (“Super Fidelity”) is a CD reviewer for Australian HiFi and Home Theatre Technology. His website is www.audaud.com.
This article was originally published in audioXpress, April 2011.





